十大經典排序算法的JS版
這世界上總存在著那么一些看似相似但有完全不同的東西,比如雷鋒和雷峰塔,小平和小平頭,瑪麗和馬里奧,Java和javascript….當年javascript為了抱Java大腿恬不知恥的讓自己變成了Java的干兒子,哦,不是應該是跪舔,畢竟都跟了Java的姓了。可如今,javascript來了個咸魚翻身,幾乎要統治web領域,Nodejs,React Native的出現使得javascript在后端和移動端都開始占有了一席之地。可以這么說,在Web的江湖,JavaScript可謂風頭無兩,已經坐上了頭把交椅。
在傳統的計算機算法和數據結構領域,大多數專業教材和書籍的默認語言都是Java或者C/C+ +,O’REILLY家倒是出了一本叫做《數據結構與算法javascript描述》的書,但不得不說,不知道是作者吃了shit還是譯者根本就沒校對,滿書的小錯誤,這就像那種無窮無盡的小bug一樣,簡直就是讓人有種嘴里塞滿了shit的感覺,吐也不是咽下去也不是。對于一個前端來說,尤其是筆試面試的時候,算法方面考的其實不難(十大排序算法或是和十大排序算法同等難度的),但就是之前沒用javascript實現過或是沒仔細看過相關算法的原理,導致寫起來浪費很多時間。所以擼一擼袖子決定自己查資料自己總結一篇博客等用到了直接看自己的博客就OK了,正所謂靠天靠地靠大牛不如靠自己(ˉ(∞)ˉ)。
算法的由來:9世紀波斯數學家提出的:“al-Khowarizmi”就是下圖這貨(感覺重要數學元素提出者貌似都戴了頂白帽子),開個玩笑,阿拉伯人對于數學史的貢獻還是值得人敬佩的。

(1)排序的定義:對一序列對象根據某個關鍵字進行排序;
輸入:n個數:a1,a2,a3,…,an
輸出:n個數的排列:a1’,a2’,a3’,…,an’,使得a1’
再講的形象點就是排排坐,調座位,高的站在后面,矮的站在前面咯。
(2)對于評述算法優劣術語的說明
穩定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
不穩定:如果a原本在b的前面,而a=b,排序之后a可能會出現在b的后面;
內排序:所有排序操作都在內存中完成;
外排序:由于數據太大,因此把數據放在磁盤中,而排序通過磁盤和內存的數據傳輸才能進行;
時間復雜度: 一個算法執行所耗費的時間。
空間復雜度: 運行完一個程序所需內存的大小。
關于時間空間復雜度的更多了解請戳這里(http://blog.csdn.net/booirror/article/details/7707551/),或是看書程杰大大編寫的《大話數據結構》還是很贊的,通俗易懂。
(3)排序算法圖片總結(圖片來源于網絡):
排序對比:
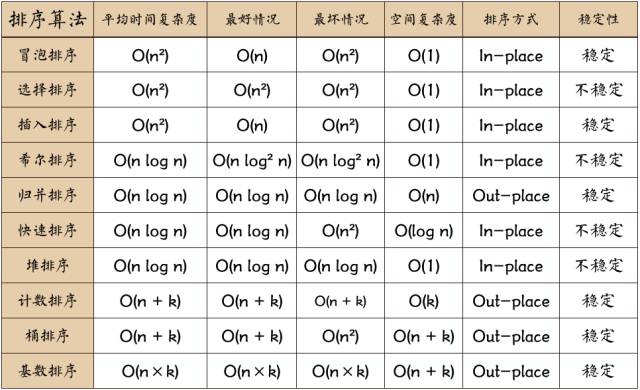
圖片名詞解釋:
n: 數據規模
k:“桶”的個數
In-place: 占用常數內存,不占用額外內存
Out-place: 占用額外內存
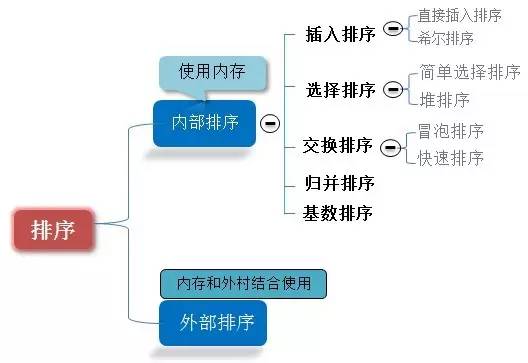
排序分類:
好的,開始總結第一個排序算法,冒泡排序。我想對于它每個學過C語言的都會了解的吧,這可能是很多人接觸的第一個排序算法。
(1)算法描述冒泡排序是一種簡單的排序算法。它重復地走訪過要排序的數列,一次比較兩個元素,如果它們的順序錯誤就把它們交換過來。走訪數列的工作是重復地進行直到沒有再需要交換,也就是說該數列已經排序完成。這個算法的名字由來是因為越小的元素會經由交換慢慢“浮”到數列的頂端。
(2)算法描述和實現具體算法描述如下:
<1>.比較相鄰的元素。如果第一個比第二個大,就交換它們兩個; <2>.對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最后一對,這樣在最后的元素應該會是最大的數; <3>.針對所有的元素重復以上的步驟,除了最后一個; <4>.重復步驟1~3,直到排序完成。JavaScript代碼實現:
function bubbleSort(arr) { var len = arr.length; for (var i = 0; i < len; i++) { for (var j = 0; j < len - 1 - i; j++) { if (arr[j] > arr[j+1]) {//相鄰元素兩兩對比 var temp = arr[j+1];//元素交換 arr[j+1] = arr[j]; arr[j] = temp; } } } return arr; } var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]; console.log(bubbleSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
改進冒泡排序:設置一標志性變量pos,用于記錄每趟排序中最后一次進行交換的位置。由于pos位置之后的記錄均已交換到位,故在進行下一趟排序時只要掃描到pos位置即可。
改進后算法如下:
function bubbleSort2(arr) { console.time(’改進后冒泡排序耗時’); var i = arr.length-1; //初始時,最后位置保持不變 while ( i> 0) { var pos= 0; //每趟開始時,無記錄交換 for (var j= 0; j< i; j++) if (arr[j]> arr[j+1]) { pos= j; //記錄交換的位置 var tmp = arr[j]; arr[j]=arr[j+1];arr[j+1]=tmp; } i= pos; //為下一趟排序作準備 } console.timeEnd(’改進后冒泡排序耗時’); return arr; } var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]; console.log(bubbleSort2(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
傳統冒泡排序中每一趟排序操作只能找到一個最大值或最小值,我們考慮利用在每趟排序中進行正向和反向兩遍冒泡的方法一次可以得到兩個最終值(最大者和最小者) , 從而使排序趟數幾乎減少了一半。
改進后的算法實現為:
function bubbleSort3(arr3) { var low = 0; var high= arr.length-1; //設置變量的初始值 var tmp,j; console.time(’2.改進后冒泡排序耗時’); while (low < high) { for (j= low; j< high; ++j) //正向冒泡,找到最大者 if (arr[j]> arr[j+1]) { tmp = arr[j]; arr[j]=arr[j+1];arr[j+1]=tmp; } --high; //修改high值, 前移一位 for (j=high; j>low; --j) //反向冒泡,找到最小者 if (arr[j]<arr[j-1]) { tmp = arr[j]; arr[j]=arr[j-1];arr[j-1]=tmp; } ++low; //修改low值,后移一位 } console.timeEnd(’2.改進后冒泡排序耗時’); return arr3; } var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]; console.log(bubbleSort3(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
三種方法耗時對比:
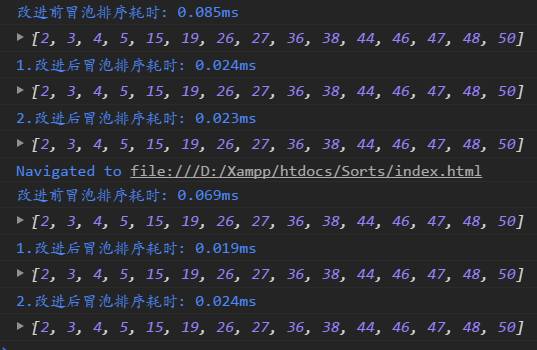
由圖可以看出改進后的冒泡排序明顯的時間復雜度更低,耗時更短了。讀者自行嘗試可以戳這,博主在github建了個庫,讀者可以Clone下來本地嘗試。此博文配合源碼體驗更棒哦~~~
冒泡排序動圖演示:
當輸入的數據已經是正序時(都已經是正序了,為毛何必還排序呢….)
最差情況:T(n) = O(n2)當輸入的數據是反序時(臥槽,我直接反序不就完了….)
平均情況:T(n) = O(n2) 2.選擇排序(Selection Sort)表現最穩定的排序算法之一(這個穩定不是指算法層面上的穩定哈,相信聰明的你能明白我說的意思2333),因為無論什么數據進去都是O(n2)的時間復雜度…..所以用到它的時候,數據規模越小越好。唯一的好處可能就是不占用額外的內存空間了吧。理論上講,選擇排序可能也是平時排序一般人想到的最多的排序方法了吧。
(1)算法簡介選擇排序(Selection-sort)是一種簡單直觀的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再從剩余未排序元素中繼續尋找最小(大)元素,然后放到已排序序列的末尾。以此類推,直到所有元素均排序完畢。
(2)算法描述和實現n個記錄的直接選擇排序可經過n-1趟直接選擇排序得到有序結果。具體算法描述如下:
<1>.初始狀態:無序區為R[1..n],有序區為空; <2>.第i趟排序(i=1,2,3…n-1)開始時,當前有序區和無序區分別為R[1..i-1]和R(i..n)。該趟排序從當前無序區中-選出關鍵字最小的記錄 R[k],將它與無序區的第1個記錄R交換,使R[1..i]和R[i+1..n)分別變為記錄個數增加1個的新有序區和記錄個數減少1個的新無序區; <3>.n-1趟結束,數組有序化了。Javascript代碼實現:
function selectionSort(arr) { var len = arr.length; var minIndex, temp; console.time(’選擇排序耗時’); for (var i = 0; i < len - 1; i++) { minIndex = i; for (var j = i + 1; j < len; j++) { if (arr[j] < arr[minIndex]) { //尋找最小的數 minIndex = j; //將最小數的索引保存 } } temp = arr[i]; arr[i] = arr[minIndex]; arr[minIndex] = temp; } console.timeEnd(’選擇排序耗時’); return arr; } var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]; console.log(selectionSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
選擇排序動圖演示:
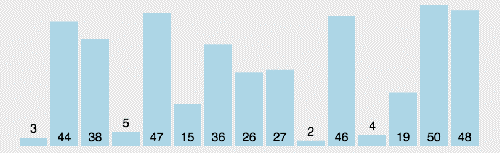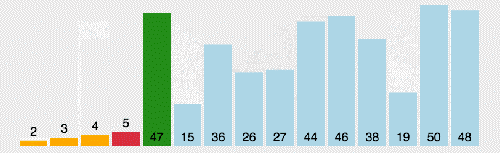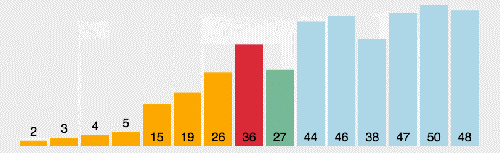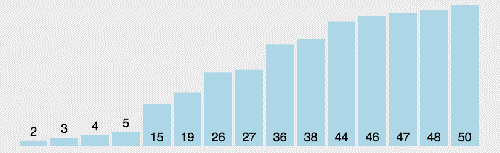
插入排序的代碼實現雖然沒有冒泡排序和選擇排序那么簡單粗暴,但它的原理應該是最容易理解的了,因為只要打過撲克牌的人都應該能夠秒懂。當然,如果你說你打撲克牌摸牌的時候從來不按牌的大小整理牌,那估計這輩子你對插入排序的算法都不會產生任何興趣了…..
(1)算法簡介插入排序(Insertion-Sort)的算法描述是一種簡單直觀的排序算法。它的工作原理是通過構建有序序列,對于未排序數據,在已排序序列中從后向前掃描,找到相應位置并插入。插入排序在實現上,通常采用in-place排序(即只需用到O(1)的額外空間的排序),因而在從后向前掃描過程中,需要反復把已排序元素逐步向后挪位,為最新元素提供插入空間。
(2)算法描述和實現一般來說,插入排序都采用in-place在數組上實現。具體算法描述如下:
<1>.從第一個元素開始,該元素可以認為已經被排序; <2>.取出下一個元素,在已經排序的元素序列中從后向前掃描; <3>.如果該元素(已排序)大于新元素,將該元素移到下一位置; <4>.重復步驟3,直到找到已排序的元素小于或者等于新元素的位置; <5>.將新元素插入到該位置后; <6>.重復步驟2~5。Javascript代碼實現:
function insertionSort(array) { if (Object.prototype.toString.call(array).slice(8, -1) === ’Array’) { console.time(’插入排序耗時:’); for (var i = 1; i < array.length; i++) { var key = array[i]; var j = i - 1; while (j >= 0 && array[j] > key) { array[j + 1] = array[j]; j--; } array[j + 1] = key; } console.timeEnd(’插入排序耗時:’); return array; } else { return ’array is not an Array!’; } }
改進插入排序:查找插入位置時使用二分查找的方式
function binaryInsertionSort(array) { if (Object.prototype.toString.call(array).slice(8, -1) === ’Array’) { console.time(’二分插入排序耗時:’); for (var i = 1; i < array.length; i++) { var key = array[i], left = 0, right = i - 1; while (left <= right) { var middle = parseInt((left + right) / 2); if (key < array[middle]) { right = middle - 1; } else { left = middle + 1; } } for (var j = i - 1; j >= left; j--) { array[j + 1] = array[j]; } array[left] = key; } console.timeEnd(’二分插入排序耗時:’); return array; } else { return ’array is not an Array!’; } } var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]; console.log(binaryInsertionSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
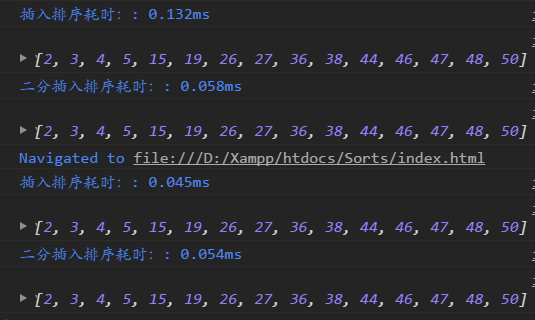
改進前后對比:
插入排序動圖演示:
1959年Shell發明;
第一個突破O(n^2)的排序算法;是簡單插入排序的改進版;它與插入排序的不同之處在于,它會優先比較距離較遠的元素。希爾排序又叫縮小增量排序
(1)算法簡介希爾排序的核心在于間隔序列的設定。既可以提前設定好間隔序列,也可以動態的定義間隔序列。動態定義間隔序列的算法是《算法(第4版》的合著者Robert Sedgewick提出的。
(2)算法描述和實現先將整個待排序的記錄序列分割成為若干子序列分別進行直接插入排序,具體算法描述:
<1>. 選擇一個增量序列t1,t2,…,tk,其中ti>tj,tk=1; <2>.按增量序列個數k,對序列進行k 趟排序; <3>.每趟排序,根據對應的增量ti,將待排序列分割成若干長度為m 的子序列,分別對各子表進行直接插入排序。僅增量因子為1 時,整個序列作為一個表來處理,表長度即為整個序列的長度。Javascript代碼實現:
function shellSort(arr) { var len = arr.length, temp, gap = 1; console.time(’希爾排序耗時:’); while(gap < len/5) { //動態定義間隔序列 gap =gap*5+1; } for (gap; gap > 0; gap = Math.floor(gap/5)) { for (var i = gap; i < len; i++) { temp = arr[i]; for (var j = i-gap; j >= 0 && arr[j] > temp; j-=gap) { arr[j+gap] = arr[j]; } arr[j+gap] = temp; } } console.timeEnd(’希爾排序耗時:’); return arr; } var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]; console.log(shellSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
希爾排序圖示(圖片來源網絡):

和選擇排序一樣,歸并排序的性能不受輸入數據的影響,但表現比選擇排序好的多,因為始終都是O(n log n)的時間復雜度。代價是需要額外的內存空間。
(1)算法簡介歸并排序是建立在歸并操作上的一種有效的排序算法。該算法是采用分治法(Divide and Conquer)的一個非常典型的應用。歸并排序是一種穩定的排序方法。將已有序的子序列合并,得到完全有序的序列;即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合并成一個有序表,稱為2-路歸并。
(2)算法描述和實現具體算法描述如下:
<1>.把長度為n的輸入序列分成兩個長度為n/2的子序列; <2>.對這兩個子序列分別采用歸并排序; <3>.將兩個排序好的子序列合并成一個最終的排序序列。Javscript代碼實現:
function mergeSort(arr) { //采用自上而下的遞歸方法 var len = arr.length; if(len < 2) { return arr; } var middle = Math.floor(len / 2), left = arr.slice(0, middle), right = arr.slice(middle); return merge(mergeSort(left), mergeSort(right)); } function merge(left, right) { var result = []; console.time(’歸并排序耗時’); while (left.length && right.length) { if (left[0] <= right[0]) { result.push(left.shift()); } else { result.push(right.shift()); } } while (left.length) result.push(left.shift()); while (right.length) result.push(right.shift()); console.timeEnd(’歸并排序耗時’); return result; } var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]; console.log(mergeSort(arr));
歸并排序動圖演示:
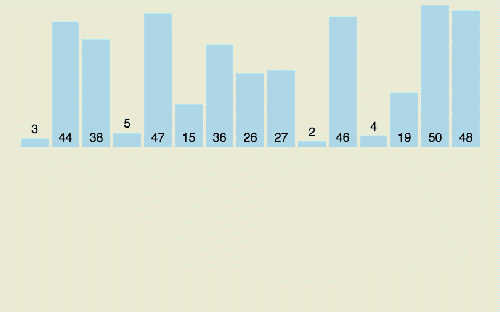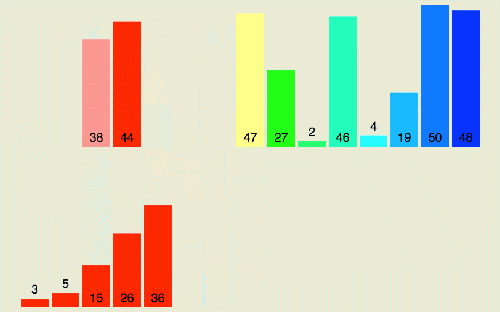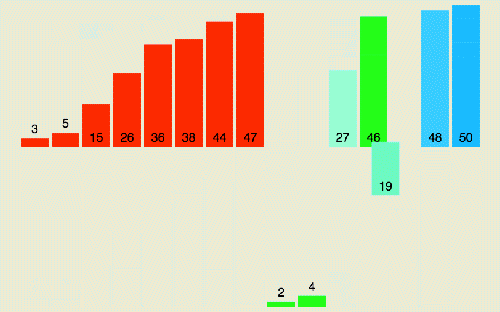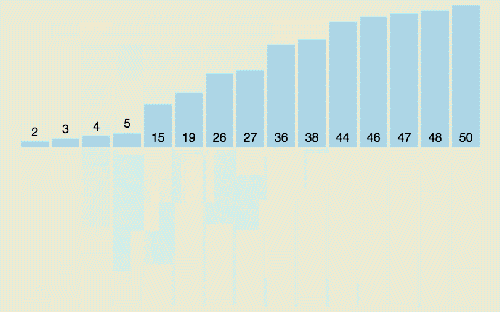
快速排序的名字起的是簡單粗暴,因為一聽到這個名字你就知道它存在的意義,就是快,而且效率高! 它是處理大數據最快的排序算法之一了。
(1)算法簡介快速排序的基本思想:通過一趟排序將待排記錄分隔成獨立的兩部分,其中一部分記錄的關鍵字均比另一部分的關鍵字小,則可分別對這兩部分記錄繼續進行排序,以達到整個序列有序。
(2)算法描述和實現快速排序使用分治法來把一個串(list)分為兩個子串(sub-lists)。具體算法描述如下:
<1>.從數列中挑出一個元素,稱為 “基準”(pivot); <2>.重新排序數列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的后面(相同的數可以到任一邊)。在這個分區退出之后,該基準就處于數列的中間位置。這個稱為分區(partition)操作; <3>.遞歸地(recursive)把小于基準值元素的子數列和大于基準值元素的子數列排序。Javascript代碼實現:/*方法說明:快速排序@param array 待排序數組*///方法一function quickSort(array, left, right) { console.time(’1.快速排序耗時’); if (Object.prototype.toString.call(array).slice(8, -1) === ’Array’ && typeof left === ’number’ && typeof right === ’number’) {if (left < right) { var x = array[right], i = left - 1, temp; for (var j = left; j <= right; j++) {if (array[j] <= x) { i++; temp = array[i]; array[i] = array[j]; array[j] = temp;} } quickSort(array, left, i - 1); quickSort(array, i + 1, right);}console.timeEnd(’1.快速排序耗時’);return array; } else {return ’array is not an Array or left or right is not a number!’; }}//方法二var quickSort2 = function(arr) { console.time(’2.快速排序耗時’);if (arr.length <= 1) { return arr; }var pivotIndex = Math.floor(arr.length / 2);var pivot = arr.splice(pivotIndex, 1)[0];var left = [];var right = [];for (var i = 0; i < arr.length; i++){if (arr[i] < pivot) {left.push(arr[i]);} else {right.push(arr[i]);}}console.timeEnd(’2.快速排序耗時’);return quickSort2(left).concat([pivot], quickSort2(right));};var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];console.log(quickSort(arr,0,arr.length-1));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]console.log(quickSort2(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
快速排序動圖演示:
堆排序可以說是一種利用堆的概念來排序的選擇排序。
(1)算法簡介堆排序(Heapsort)是指利用堆這種數據結構所設計的一種排序算法。堆積是一個近似完全二叉樹的結構,并同時滿足堆積的性質:即子結點的鍵值或索引總是小于(或者大于)它的父節點。
(2)算法描述和實現具體算法描述如下:
<1>.將初始待排序關鍵字序列(R1,R2….Rn)構建成大頂堆,此堆為初始的無序區; <2>.將堆頂元素R[1]與最后一個元素R[n]交換,此時得到新的無序區(R1,R2,……Rn-1)和新的有序區(Rn),且滿足R[1,2…n-1]<=R[n]; <3>.由于交換后新的堆頂R[1]可能違反堆的性質,因此需要對當前無序區(R1,R2,……Rn-1)調整為新堆,然后再次將R[1]與無序區最后一個元素交換,得到新的無序區(R1,R2….Rn-2)和新的有序區(Rn-1,Rn)。不斷重復此過程直到有序區的元素個數為n-1,則整個排序過程完成。Javascript代碼實現:
/*方法說明:堆排序@param array 待排序數組*/function heapSort(array) { console.time(’堆排序耗時’); if (Object.prototype.toString.call(array).slice(8, -1) === ’Array’) {//建堆var heapSize = array.length, temp;for (var i = Math.floor(heapSize / 2) - 1; i >= 0; i--) { heapify(array, i, heapSize);}//堆排序for (var j = heapSize - 1; j >= 1; j--) { temp = array[0]; array[0] = array[j]; array[j] = temp; heapify(array, 0, --heapSize);}console.timeEnd(’堆排序耗時’);return array; } else {return ’array is not an Array!’; }}/*方法說明:維護堆的性質@param arr 數組@param x 數組下標@param len 堆大小*/function heapify(arr, x, len) { if (Object.prototype.toString.call(arr).slice(8, -1) === ’Array’ && typeof x === ’number’) {var l = 2 * x + 1, r = 2 * x + 2, largest = x, temp;if (l < len && arr[l] > arr[largest]) { largest = l;}if (r < len && arr[r] > arr[largest]) { largest = r;}if (largest != x) { temp = arr[x]; arr[x] = arr[largest]; arr[largest] = temp; heapify(arr, largest, len);} } else {return ’arr is not an Array or x is not a number!’; }}var arr=[91,60,96,13,35,65,46,65,10,30,20,31,77,81,22];console.log(heapSort(arr));//[10, 13, 20, 22, 30, 31, 35, 46, 60, 65, 65, 77, 81, 91, 96]
堆排序動圖演示:

計數排序的核心在于將輸入的數據值轉化為鍵存儲在額外開辟的數組空間中。
作為一種線性時間復雜度的排序,計數排序要求輸入的數據必須是有確定范圍的整數。
(1)算法簡介計數排序(Counting sort)是一種穩定的排序算法。計數排序使用一個額外的數組C,其中第i個元素是待排序數組A中值等于i的元素的個數。然后根據數組C來將A中的元素排到正確的位置。它只能對整數進行排序。
(2)算法描述和實現具體算法描述如下:
<1>. 找出待排序的數組中最大和最小的元素; <2>. 統計數組中每個值為i的元素出現的次數,存入數組C的第i項; <3>. 對所有的計數累加(從C中的第一個元素開始,每一項和前一項相加); <4>. 反向填充目標數組:將每個元素i放在新數組的第C(i)項,每放一個元素就將C(i)減去1。Javascript代碼實現:
function countingSort(array) { var len = array.length,B = [],C = [],min = max = array[0]; console.time(’計數排序耗時’); for (var i = 0; i < len; i++) {min = min <= array[i] ? min : array[i];max = max >= array[i] ? max : array[i];C[array[i]] = C[array[i]] ? C[array[i]] + 1 : 1; } for (var j = min; j < max; j++) {C[j + 1] = (C[j + 1] || 0) + (C[j] || 0); } for (var k = len - 1; k >= 0; k--) {B[C[array[k]] - 1] = array[k];C[array[k]]--; } console.timeEnd(’計數排序耗時’); return B;}var arr = [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2];console.log(countingSort(arr)); //[1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 6, 7, 7, 8, 8, 9, 9]
JavaScript動圖演示:
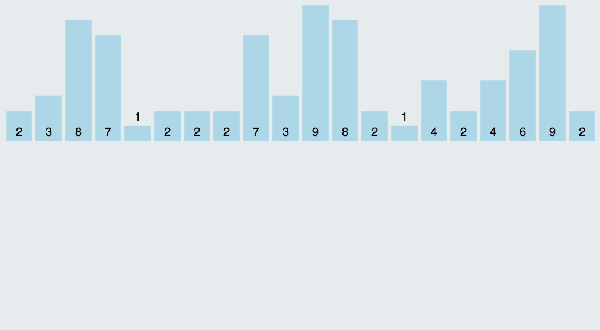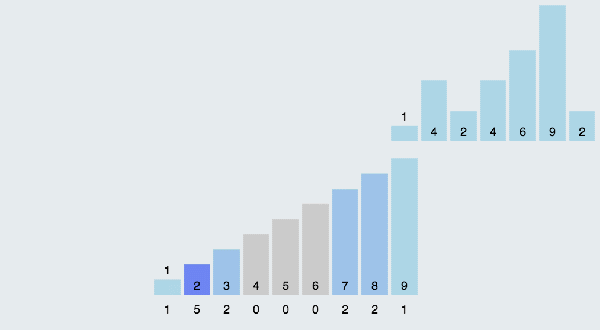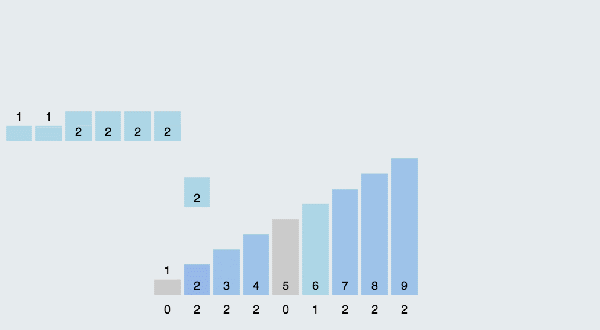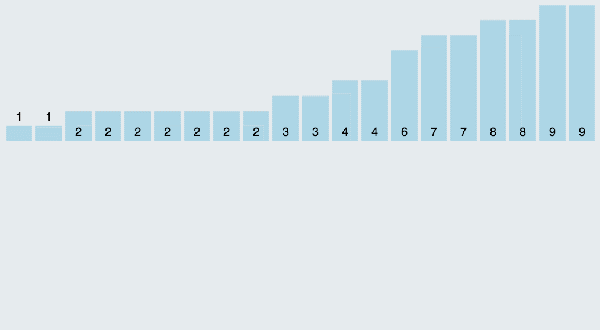
當輸入的元素是n 個0到k之間的整數時,它的運行時間是 O(n + k)。計數排序不是比較排序,排序的速度快于任何比較排序算法。由于用來計數的數組C的長度取決于待排序數組中數據的范圍(等于待排序數組的最大值與最小值的差加上1),這使得計數排序對于數據范圍很大的數組,需要大量時間和內存。
最佳情況:T(n) = O(n+k) 最差情況:T(n) = O(n+k) 平均情況:T(n) = O(n+k) 9.桶排序(Bucket Sort)桶排序是計數排序的升級版。它利用了函數的映射關系,高效與否的關鍵就在于這個映射函數的確定。
(1)算法簡介桶排序 (Bucket sort)的工作的原理:假設輸入數據服從均勻分布,將數據分到有限數量的桶里,每個桶再分別排序(有可能再使用別的排序算法或是以遞歸方式繼續使用桶排序進行排
(2)算法描述和實現具體算法描述如下:
<1>.設置一個定量的數組當作空桶; <2>.遍歷輸入數據,并且把數據一個一個放到對應的桶里去; <3>.對每個不是空的桶進行排序; <4>.從不是空的桶里把排好序的數據拼接起來。Javascript代碼實現:
/*方法說明:桶排序@param array 數組@param num 桶的數量*/function bucketSort(array, num) { if (array.length <= 1) {return array; } var len = array.length, buckets = [], result = [], min = max = array[0], regex = ’/^[1-9]+[0-9]*$/’, space, n = 0; num = num || ((num > 1 && regex.test(num)) ? num : 10); console.time(’桶排序耗時’); for (var i = 1; i < len; i++) {min = min <= array[i] ? min : array[i];max = max >= array[i] ? max : array[i]; } space = (max - min + 1) / num; for (var j = 0; j < len; j++) {var index = Math.floor((array[j] - min) / space);if (buckets[index]) { // 非空桶,插入排序 var k = buckets[index].length - 1; while (k >= 0 && buckets[index][k] > array[j]) {buckets[index][k + 1] = buckets[index][k];k--; } buckets[index][k + 1] = array[j];} else { //空桶,初始化 buckets[index] = []; buckets[index].push(array[j]);} } while (n < num) {result = result.concat(buckets[n]);n++; } console.timeEnd(’桶排序耗時’); return result;}var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];console.log(bucketSort(arr,4));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
桶排序圖示(圖片來源網絡):
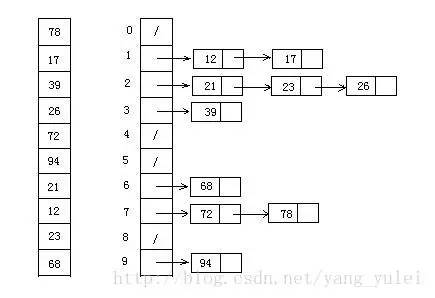
桶排序最好情況下使用線性時間O(n),桶排序的時間復雜度,取決與對各個桶之間數據進行排序的時間復雜度,因為其它部分的時間復雜度都為O(n)。很顯然,桶劃分的越小,各個桶之間的數據越少,排序所用的時間也會越少。但相應的空間消耗就會增大。
最佳情況:T(n) = O(n+k) 最差情況:T(n) = O(n+k) 平均情況:T(n) = O(n2) 10.基數排序(Radix Sort)基數排序也是非比較的排序算法,對每一位進行排序,從最低位開始排序,復雜度為O(kn),為數組長度,k為數組中的數的最大的位數;
(1)算法簡介基數排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次類推,直到最高位。有時候有些屬性是有優先級順序的,先按低優先級排序,再按高優先級排序。最后的次序就是高優先級高的在前,高優先級相同的低優先級高的在前。基數排序基于分別排序,分別收集,所以是穩定的。
(2)算法描述和實現具體算法描述如下:
<1>.取得數組中的最大數,并取得位數; <2>.arr為原始數組,從最低位開始取每個位組成radix數組; <3>.對radix進行計數排序(利用計數排序適用于小范圍數的特點);Javascript代碼實現:
/** * 基數排序適用于: * (1)數據范圍較小,建議在小于1000 * (2)每個數值都要大于等于0 * @author xiazdong * @param arr 待排序數組 * @param maxDigit 最大位數 *///LSD Radix Sortfunction radixSort(arr, maxDigit) { var mod = 10; var dev = 1; var counter = []; console.time(’基數排序耗時’); for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {for(var j = 0; j < arr.length; j++) { var bucket = parseInt((arr[j] % mod) / dev); if(counter[bucket]== null) {counter[bucket] = []; } counter[bucket].push(arr[j]);}var pos = 0;for(var j = 0; j < counter.length; j++) { var value = null; if(counter[j]!=null) {while ((value = counter[j].shift()) != null) { arr[pos++] = value;} }} } console.timeEnd(’基數排序耗時’); return arr;}var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];console.log(radixSort(arr,2)); //[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
基數排序LSD動圖演示:
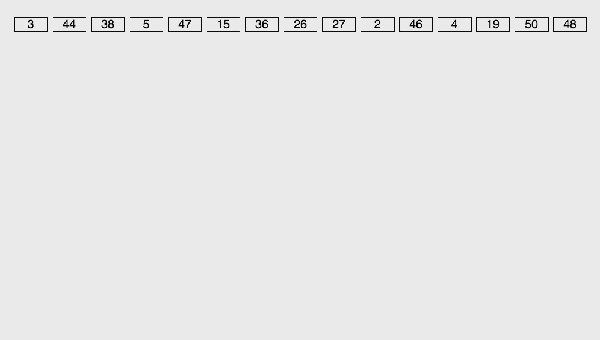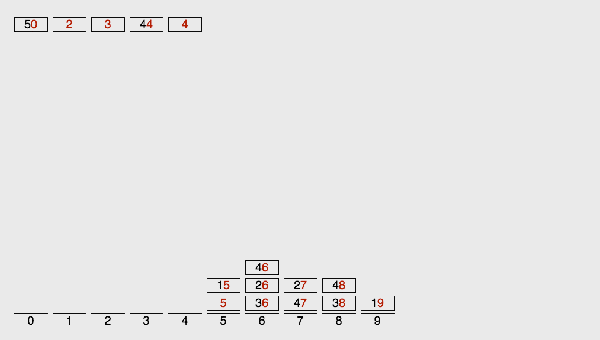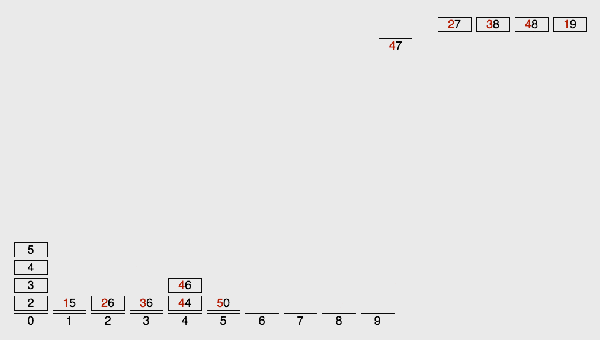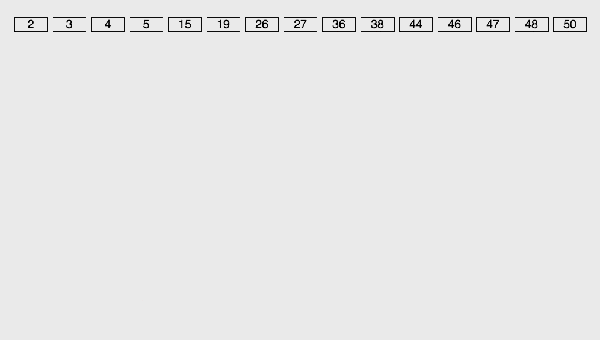
基數排序有兩種方法:
MSD 從高位開始進行排序 LSD 從低位開始進行排序基數排序 vs 計數排序 vs 桶排序
這三種排序算法都利用了桶的概念,但對桶的使用方法上有明顯差異:
基數排序:根據鍵值的每位數字來分配桶 計數排序:每個桶只存儲單一鍵值 桶排序:每個桶存儲一定范圍的數值 后記十大排序算法的總結到這里就算告一段落了。博主總結完之后只有一個感覺,排序算法博大精深,前輩們用了數年甚至一輩子的心血研究出來的算法更值得我們推敲。站在十大算法的門前心里還是誠惶誠恐的,身為一個小學生,博主的總結難免會有所疏漏,歡迎各位批評指正。
項目主頁:http://www.open-open.com/lib/view/home/1500369363693
相關文章:

 網公網安備
網公網安備