目錄一、前言二、淺談遞歸三、回溯算法四、八皇后問題五、八皇后變種六、總結(jié)一、前言

說起八皇后問題，它是一道回溯算法類的經(jīng)典問題，也可能是我們大部分人在上數(shù)據(jù)結(jié)構(gòu)或者算法課上遇到過的最難的一道題……

二、淺談遞歸

對(duì)于遞歸算法，我覺得掌握遞歸是入門數(shù)據(jù)結(jié)構(gòu)與算法的關(guān)鍵，因?yàn)楹竺鎸W(xué)習(xí)很多操作涉及到遞歸，例如鏈表的一些操作、樹的遍歷和一些操作、圖的dfs、快排、歸并排序等等。

遞歸的實(shí)質(zhì)還是借助棧實(shí)現(xiàn)一些操作，利用遞歸能夠完成的操作使用棧都能夠完成，并且利用棧的話可以很好的控制停止，效率更高(遞歸是一個(gè)來回的過程回來的時(shí)候需要特判)。

遞歸實(shí)現(xiàn)和棧實(shí)現(xiàn)操作的區(qū)別，遞歸對(duì)我們來說更簡(jiǎn)潔巧妙，并且用多了會(huì)發(fā)現(xiàn)很多問題的處理上遞歸的思考方式更偏向人的思考方式，而棧的話就是老老實(shí)實(shí)用計(jì)算機(jī)(數(shù)據(jù)結(jié)構(gòu)特性)的思維去思考問題。這個(gè)你可以參考二叉樹的遍歷方式遞歸和非遞歸版本，復(fù)雜性一目了然。

從遞歸算法的特征上來看，遞歸算法的問題都是父問題可以用過一定關(guān)系轉(zhuǎn)化為子問題。即從后往前推導(dǎo)的過程，一般通過一個(gè)參數(shù)來表示當(dāng)前的層級(jí)。

而遞歸的主要特點(diǎn)如下：

自己調(diào)用自己 遞歸通常不在意具體操作，只關(guān)心初始條件和上下層的變化關(guān)系。 遞歸函數(shù)需要有臨界停止點(diǎn)，即遞歸不能無限制的執(zhí)行下去。通常這個(gè)點(diǎn)為必須經(jīng)過的一個(gè)數(shù)。 遞歸可以被棧替代。有些遞歸可以優(yōu)化。比如遇到重復(fù)性的可以借助空間內(nèi)存記錄而減少遞歸的次數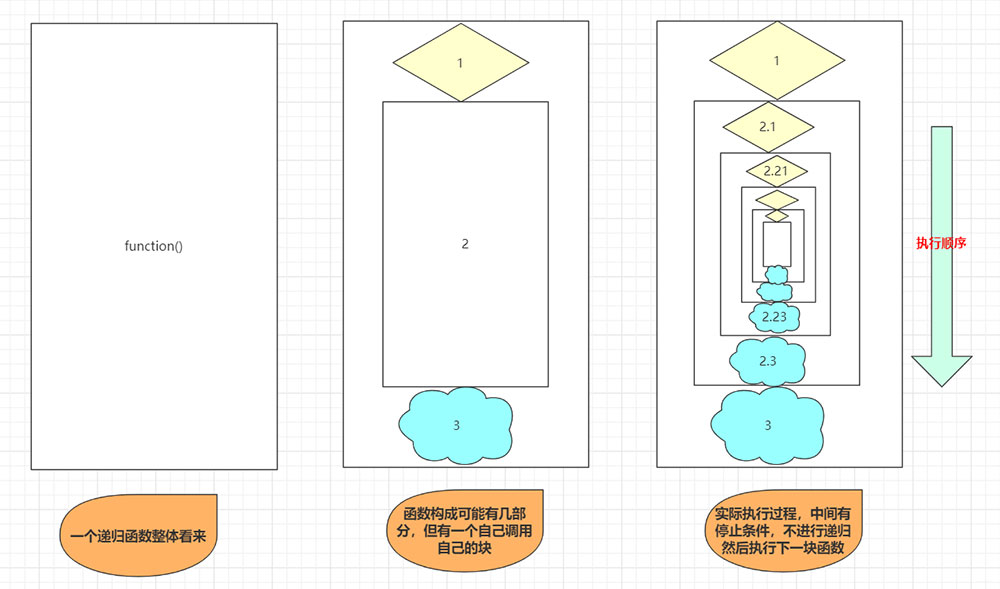(shù)。

而通常遞歸算法的一個(gè)流程大致為：

定義遞歸算法及參數(shù)

- 停止遞歸算法條件

- (可存在)其他邏輯

- 遞歸調(diào)用(參數(shù)需要改變)

- (可存在)其他邏輯

三、回溯算法

談完遞歸，你可能明白有這么一種方法可以使用，但你可能感覺單單的遞歸和八皇后還是很難扯上關(guān)系，是的沒錯(cuò)，所以我來講回溯算法了。

算法界中，有五大常用算法：貪心算法、分治算法、動(dòng)態(tài)規(guī)劃算法、回溯算法、分支界限算法。咱們回溯算法就是五大之一，因?yàn)榛厮菟惴軌蚪鉀Q很多實(shí)際的問題，盡管很多時(shí)候復(fù)雜度可能不太小，但大部分情況都能得到一個(gè)不錯(cuò)的結(jié)果。

對(duì)于回溯法的定義，百度百科是這么定義的：

回溯算法實(shí)際上一個(gè)類似枚舉的搜索嘗試過程，主要是在搜索嘗試過程中尋找問題的解，當(dāng)發(fā)現(xiàn)已不滿足求解條件時(shí)，就“回溯”返回，嘗試別的路徑。回溯法是一種選優(yōu)搜索法，按選優(yōu)條件向前搜索，以達(dá)到目標(biāo)。但當(dāng)探索到某一步時(shí)，發(fā)現(xiàn)原先選擇并不優(yōu)或達(dá)不到目標(biāo)，就退回一步重新選擇，這種走不通就退回再走的技術(shù)為回溯法，而滿足回溯條件的某個(gè)狀態(tài)的點(diǎn)稱為“回溯點(diǎn)”。許多復(fù)雜的，規(guī)模較大的問題都可以使用回溯法，有“通用解題方法”的美稱。

對(duì)于回溯法，它的核心就是試探和復(fù)原。這個(gè)自動(dòng)化的過程就是利用遞歸去執(zhí)行，在遞歸函數(shù)執(zhí)行前去修改嘗試，滿足條件后向下遞歸試探，試探完畢后需要將數(shù)值復(fù)原。在這個(gè)試探的過程中找到我們所需要的一個(gè)或者所有解。這個(gè)我們也俗稱暴力。

啥？沒聽懂？好，那我就再講講，你應(yīng)該知道深度優(yōu)先搜索(dfs)吧？其實(shí)回溯算法就是一種特殊的dfs。之所以叫回溯，就是因?yàn)檫@類算法在運(yùn)用遞歸都有個(gè)復(fù)原的過程，所以前面的操作就相當(dāng)于試探一樣。而這類算法一般常常配對(duì)一個(gè)或多個(gè)boolean類型的數(shù)組用來標(biāo)記試探途中用過的點(diǎn)。

舉個(gè)例子，我們知道回溯算法用來求所有數(shù)字的排列順序。我們分析其中一個(gè)順序。比如數(shù)列6 8 9這個(gè)序列的話，我們用來求它的排列順序。

對(duì)于代碼塊來說，這可能很容易實(shí)現(xiàn)：

import java.util.Arrays;public class test { public static void main(String[] args) {int arr[]={6,8,9};//需要排列組合的數(shù)組int val[]={0,0,0};//臨時(shí)儲(chǔ)存的數(shù)組boolean jud[] = new boolean[arr.length];// 判斷是否被用dfs(arr,val, jud, 0,'');//用一個(gè)字符串長度更直觀看結(jié)果 } private static void dfs(int[] arr, int val[],boolean[] jud, int index,String s) {System.out.println(s+Arrays.toString(val));if (index == arr.length){ }//停止遞歸條件else{ for (int i = 0; i < arr.length; i++) {if (!jud[i]) {//當(dāng)前不能用的 int team=val[index]; val[index] = arr[i]; jud[i] = true;// 下層不能在用 dfs(arr, val, jud, index + 1,s+' _ '); jud[i] = false;// 還原 val[index]=team;} }} }}

而執(zhí)行的結(jié)果為：

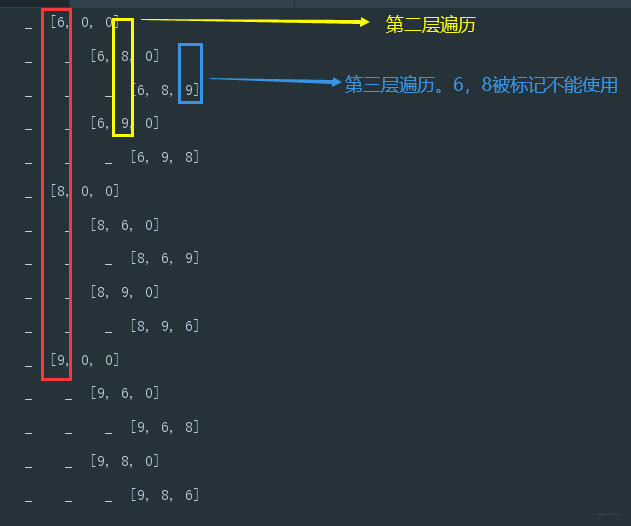
這里再配張圖理解：

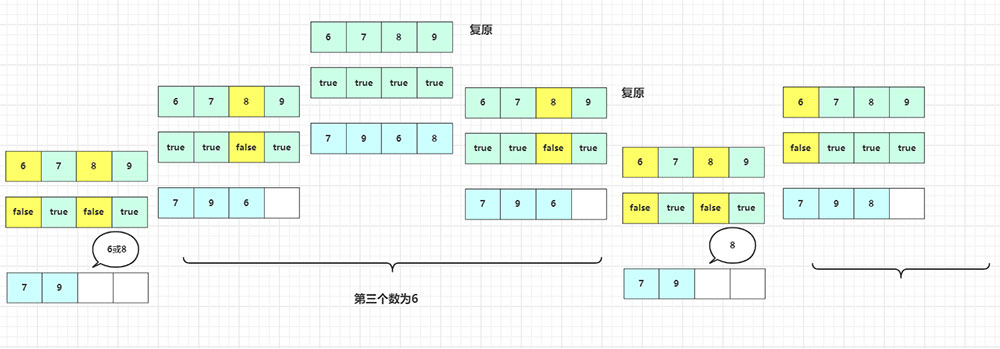
而通常回溯算法的一個(gè)流程大致為：

定義回溯算法及參數(shù)

- (符合條件)跳出

- (不符合)不跳出：

- - 遍歷需要操作的列表&&該元素可操作&&可以繼續(xù)試探

- - - 標(biāo)記該元素已使用以及其他操作

- - - 遞歸調(diào)用(參數(shù)改變)

- - - 清除該元素標(biāo)記以及其他操作

也就是在使用數(shù)組進(jìn)行回溯的時(shí)候，使用過的時(shí)候需要標(biāo)記子遞歸不能再使用防止死循環(huán)，而當(dāng)回來的時(shí)候需要解封該位置，以便該編號(hào)位置被其他兄弟使用之后這個(gè)數(shù)值在后面能夠再次使用！而如果使用List或者StringBuilder等動(dòng)態(tài)空間用來進(jìn)行回溯的時(shí)候記得同樣的復(fù)原，刪了要記得增，減了要記得加。搞明白這些，我想回溯算法也應(yīng)該難不倒你了吧。

四、八皇后問題

掌握了回溯算法的關(guān)鍵，八皇后問題多思考就可以想的出來了。前面的講解都是為了解決八皇后問題做鋪墊。首先，我們認(rèn)真的看下八皇后問題描述。

八皇后問題（英文：Eight queens），是由國際西洋棋棋手馬克斯·貝瑟爾于1848年提出的問題，是回溯算法的典型案例。

問題表述為：在8×8格的國際象棋上擺放8個(gè)皇后，使其不能互相攻擊，即任意兩個(gè)皇后都不能處于同一行、同一列或同一斜線上，問有多少種擺法。高斯認(rèn)為有76種方案。1854年在柏林的象棋雜志上不同的作者發(fā)表了40種不同的解，后來有人用圖論的方法解出92種結(jié)果。如果經(jīng)過±90度、±180度旋轉(zhuǎn)，和對(duì)角線對(duì)稱變換的擺法看成一類，共有42類。計(jì)算機(jī)發(fā)明后，有多種計(jì)算機(jī)語言可以編程解決此問題。

我們?cè)撛趺此伎歼@種問題呢?也就是從何入手呢？

從限制條件入手

八皇后問題有以下限制條件：

8 x 8的方格 每行一個(gè)，共八行(0-7) 每列一個(gè)，共八列(0-7) 每左斜杠一個(gè)，共十五左斜杠(0-14) 每右斜杠一個(gè)，共十五右斜杠(0-14)

當(dāng)看到這些限制條件，肯定想到這么多限制條件需要判斷。判斷的話當(dāng)然就是借助boolean數(shù)組啦。還是一維的8個(gè)大小，所以我們首先用4個(gè)boolean數(shù)組用來判斷各自的條件是否被滿足。

表示這個(gè)圖的話我們可以使用一個(gè)int類型數(shù)組表示，0表示沒有，1表示有皇后。

那么如何去設(shè)計(jì)這個(gè)算法呢？這個(gè)并不是每個(gè)格子都有數(shù)字，所以在進(jìn)行回溯的時(shí)候不應(yīng)該每個(gè)格子每個(gè)格子進(jìn)行向下遞歸(同行互斥)，也就是遞歸到當(dāng)前層的時(shí)候，循環(huán)遍歷該層的八種情況進(jìn)行試探(每個(gè)都試探)，如果不滿足條件的就不操作而被終止掉，但該行每個(gè)滿足條件的需要遞歸的時(shí)候需要進(jìn)入到下一行。

當(dāng)然你需要提前知道當(dāng)前位置橫縱坐標(biāo)怎們知道對(duì)應(yīng)的boolean位置(位置從0號(hào)開始計(jì)算)。例如位置p(x,y)中對(duì)應(yīng)的位置為：

hang[] :x每一行就是對(duì)應(yīng)的i。 lie[] :y每一列就是對(duì)應(yīng)的j。 zuoxie[] :x+y規(guī)定順序?yàn)樽笊系接蚁? youxie[] :x+(7-y)規(guī)定順序?yàn)橛疑系阶笙?個(gè)人習(xí)慣)

好啦，該算法的實(shí)現(xiàn)代碼為：

import java.util.Arrays;public class EightQueens { static int allnum=0; public static void main(String[] args) {boolean hang[]=new boolean[8];//行boolean lie[]=new boolean[8];//列boolean zuoxie[]=new boolean[15];//左斜杠boolean youxie[]=new boolean[15];//右斜杠int map[][]=new int[8][8];//地圖dfs(0,hang,lie,zuoxie,youxie,map);//進(jìn)行下去 } private static void dfs(int hindex, boolean[] hang, boolean[] lie, boolean[] zuoxie, boolean[] youxie, int[][] map) {if(hindex==8){ allnum++; printmap(map);//輸出map}else{ //hindex為行 i為具體的某一列 for(int i=0;i<8;i++) {if(!hang[hindex]&&!lie[i]&&!zuoxie[hindex+i]&&!youxie[hindex+(7-i)]){ hang[hindex]=true;//試探 lie[i]=true; zuoxie[hindex+i]=true; youxie[hindex+(7-i)]=true; map[hindex][i]=1; dfs(hindex+1,hang,lie,zuoxie,youxie,map);//dfs hang[hindex]=false;//還原 lie[i]=false; zuoxie[hindex+i]=false; youxie[hindex+(7-i)]=false; map[hindex][i]=0;} }} } //輸出地圖 private static void printmap(int[][] map) {System.out.println('第'+allnum+'個(gè)排列為');for(int a[]:map){ System.out.println(Arrays.toString(a));} }}

跑一邊就知道到底有多少種皇后，最終是92種皇后排列方式，不得不說能用數(shù)學(xué)方法接出來的是真的牛叉。

五、八皇后變種

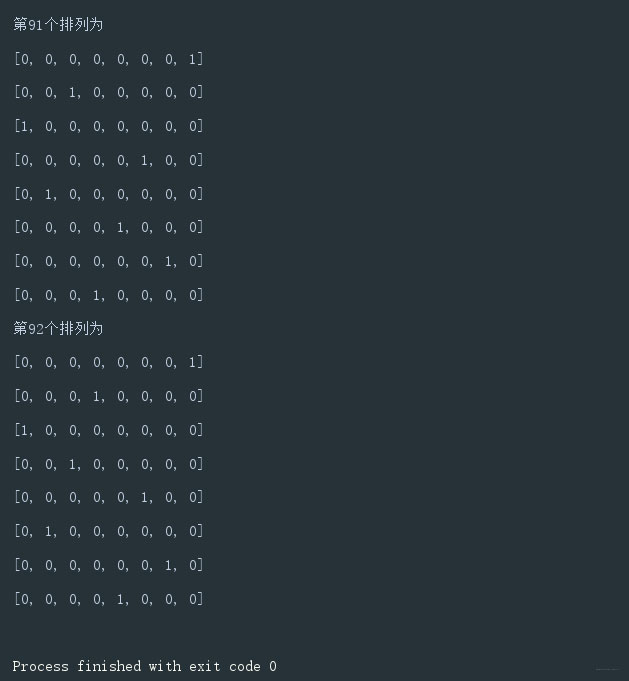
此時(shí)我想八皇后問題已經(jīng)搞得明明白白了，但是智慧的人們總是想出各種方法變化題目想難到我們，這種八皇后問題有很多變種，例如n皇后，數(shù)獨(dú)等問題。

這里就簡(jiǎn)單講講兩數(shù)獨(dú)問題的變種。

力扣36 有效的數(shù)獨(dú)

像這種題需要考慮和八皇后還是很像，改成9*9，只不過在具體處理需要考慮橫、豎和3x3小方格。

當(dāng)然這題比較簡(jiǎn)單，還有一題就比較麻煩了力扣37解數(shù)獨(dú)。

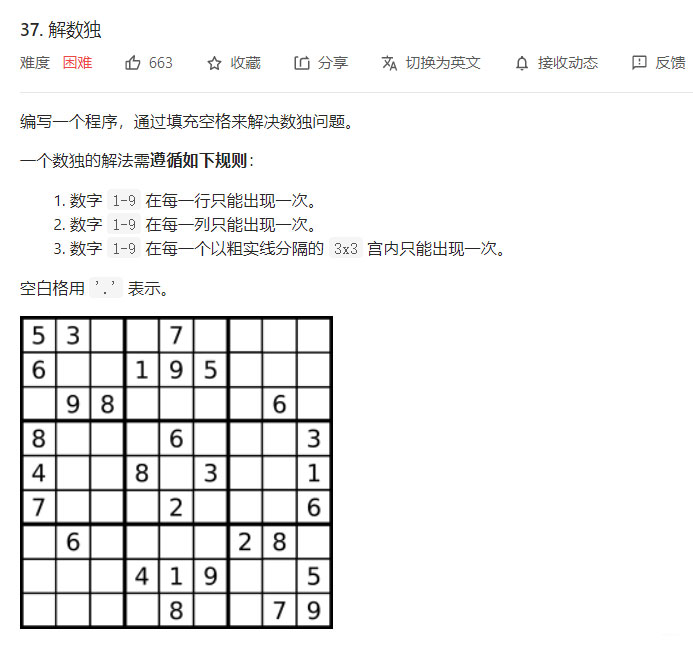
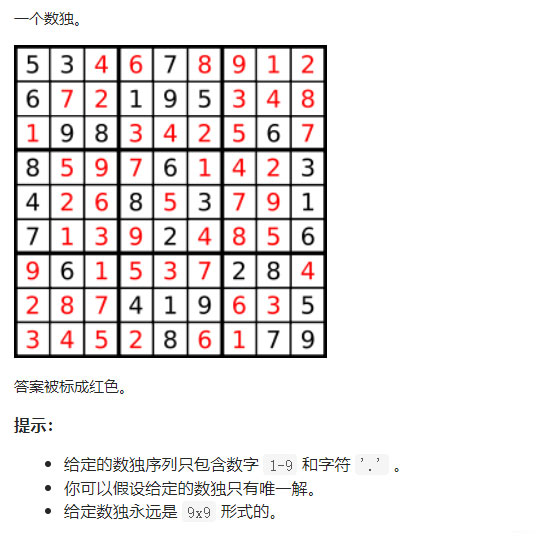
這一題有難度的就是需要我們每個(gè)位置都有數(shù)據(jù)都要去試探。

這種二維的回溯需要考慮一些問題，我們對(duì)于每一行每一行考慮。 每一行已經(jīng)預(yù)有一些數(shù)據(jù)事先標(biāo)記，在從開始試探放值，滿足條件后向下遞歸試探。一直到結(jié)束如果都滿足那么就可以結(jié)束返回?cái)?shù)組值。

這里的話有兩點(diǎn)需要注意的在這里提一下：

用二維兩個(gè)參數(shù)進(jìn)行遞歸回溯判斷起來誰加誰減比較麻煩，所以我們用一個(gè)參數(shù)index用它來計(jì)算橫縱坐標(biāo)進(jìn)行轉(zhuǎn)換，這樣就減少二維遞歸的一些麻煩。 回溯是一個(gè)來回的過程，在回來的過程正常情況需要將數(shù)據(jù)改回去，但是如果已經(jīng)知道結(jié)果就沒必要再該回去可以直接停止放置回溯造成值的修改(這里我用了一個(gè)isfinish的boolean類型進(jìn)行判斷)。

代碼可以參考為：

六、總結(jié)

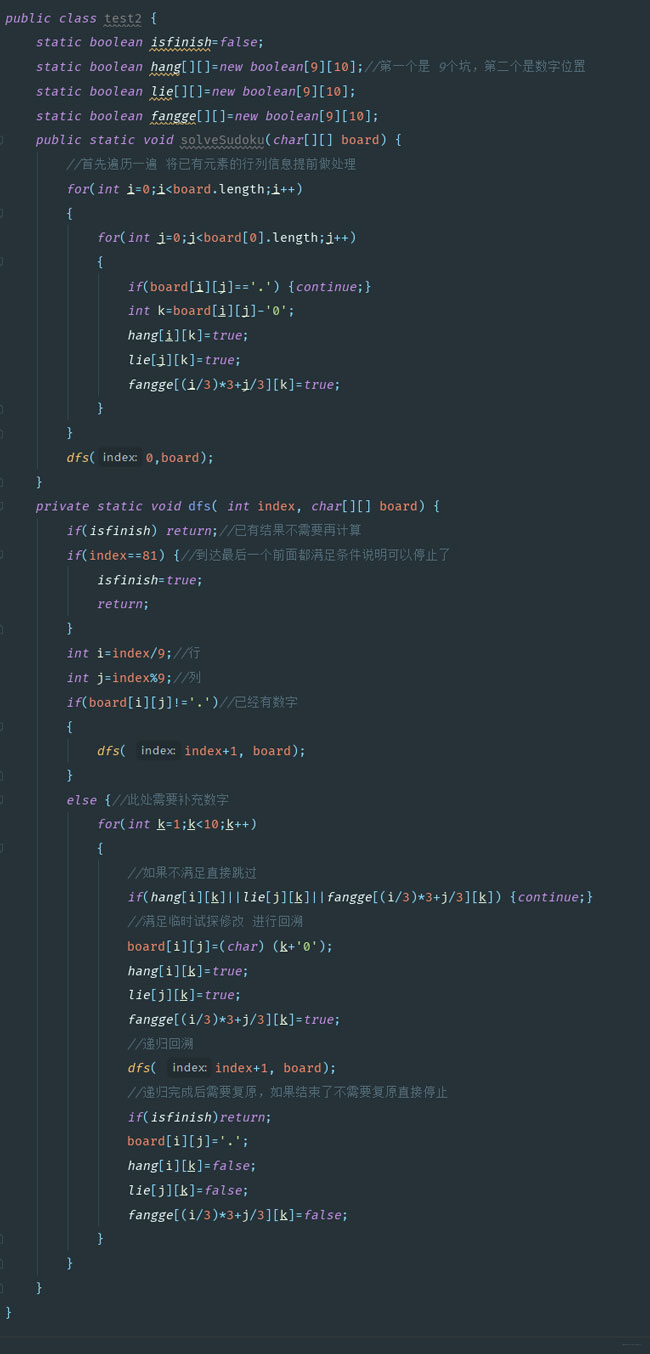
遞歸更注重一種方式，自己調(diào)用自己。回溯更注重試探和復(fù)原，這個(gè)過程一般借助遞歸。dfs深度優(yōu)先搜素，一般用棧或者遞歸去實(shí)現(xiàn)，如果用遞歸可能會(huì)復(fù)原也可能不復(fù)原數(shù)據(jù)，所以回溯是深搜的一種。八皇后是經(jīng)典回溯算法解決的問題，你說深度優(yōu)先搜素其實(shí)也沒問題，但回溯更能精準(zhǔn)的描述算法特征。

以上就是淺談Java實(shí)現(xiàn)回溯算法之八皇后問題的詳細(xì)內(nèi)容，更多關(guān)于Java 回溯算法 八皇后的資料請(qǐng)關(guān)注好吧啦網(wǎng)其它相關(guān)文章！