目錄一、背景二、放棄 hash 函數(shù)三、優(yōu)化 hash 函數(shù)3.1、評(píng)價(jià)函數(shù)3.2、訓(xùn)練策略3.3、ForkJoin 框架3.4、效果一、背景

現(xiàn)有個(gè)處理股票行情消息的系統(tǒng)，其架構(gòu)如下：

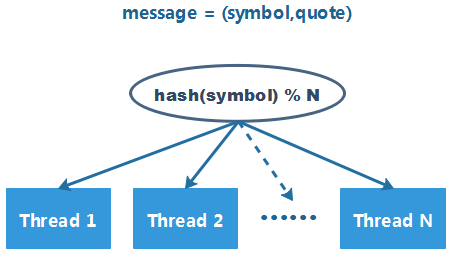
由于數(shù)據(jù)量巨大，系統(tǒng)中啟動(dòng)了 15 個(gè)線程來消費(fèi)行情消息。消息分配的策略較為簡(jiǎn)單：對(duì) symbol 的 hashCode 取模，將消息分配給其中一個(gè)線程進(jìn)行處理。 經(jīng)過驗(yàn)證，每個(gè)線程分配到的 symbol 數(shù)量較為均勻，于是系統(tǒng)愉快地上線了。

運(yùn)行一段時(shí)間后，突然收到了系統(tǒng)的告警，但此時(shí)并非消息峰值時(shí)間段。經(jīng)過排查后，發(fā)現(xiàn)問題出現(xiàn)在 hash 函數(shù)上：

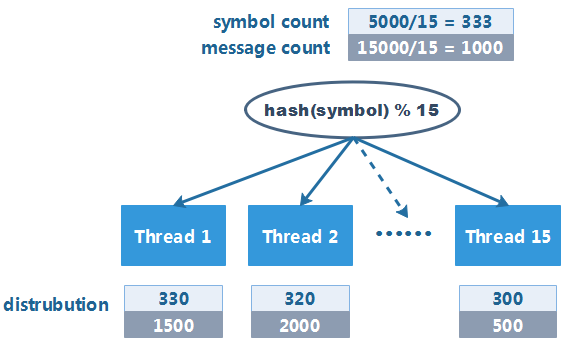
雖然每個(gè)線程被分配到的 symbol 數(shù)量較為均衡，但是部分熱門 symbol 的報(bào)價(jià)消息量會(huì)更多，如果熱門 symbol 集中到特定線程上，就會(huì)造成線程負(fù)載不均衡，使得系統(tǒng)整體的吞吐量大打折扣。

為提高系統(tǒng)的吞吐量，有必要消息分發(fā)邏輯進(jìn)行一些改造，避免出現(xiàn)熱點(diǎn)線程。為此，系統(tǒng)需要記錄下某天內(nèi)每個(gè) symbol 的消息量，然后在第二天使用這些數(shù)據(jù)，對(duì)分發(fā)邏輯進(jìn)行調(diào)整。具體的改造的方案可以分為兩種：

放棄使用 hash 函數(shù) 對(duì) hash 函數(shù)進(jìn)行優(yōu)化二、放棄 hash 函數(shù)

問題可以抽象為：

將 5000 個(gè)非負(fù)整數(shù)分配至 15 個(gè)桶(bucket)中，并盡可能保證每個(gè)桶中的元素之和接近（每個(gè)桶中的元素個(gè)數(shù)無限制）。

每個(gè)整數(shù)元素可能的放置方法有 15 種，這個(gè)問題總共可能的解有 155000種，暴力求解的可能性微乎其微。作為工程問題，最優(yōu)解不是必要的，可以退而求其次尋找一個(gè)可接受的次優(yōu)解：

根據(jù)所有 symbol 的消息總數(shù)計(jì)算一個(gè)期望的分布均值(expectation)。將每個(gè) symbol 的消息數(shù)按照 symbol 的順序進(jìn)行排列，最后將這組數(shù)組劃分為 15 個(gè)區(qū)間，并且盡可能使得每個(gè)區(qū)間元素之和與 expection 接近。使用一個(gè)有序查找表記錄每個(gè)區(qū)間的首個(gè) symbol，后續(xù)就可以按照這個(gè)表對(duì)數(shù)據(jù)進(jìn)行劃分。

public class FindBestDistribution { static final int NUM_OF_SYMBOLS = 5000; static final int NUM_OF_BUCKETS = 15; public static void main(String[] args) {// 生成樣本IntStream ints = ThreadLocalRandom.current().ints(0, 1000);PrimitiveIterator.OfInt iterator = ints.iterator();Map<String,Integer> symbolAndCount = new TreeMap<>();for (int i=0; i<NUM_OF_SYMBOLS; i++) { symbolAndCount.put(Integer.toHexString(i).toUpperCase(), iterator.next());}// 按照 symbol 劃分每個(gè)桶的數(shù)量TreeMap<String, Integer> distribution = findBestDistribution(symbolAndCount);// 測(cè)試效果int[] buckets = new int[NUM_OF_BUCKETS];for (Map.Entry<String, Integer> entry : symbolAndCount.entrySet()) { Map.Entry<String, Integer> floor = distribution.floorEntry(entry.getKey()); int bucketIndex = floor == null ? 0 : floor.getValue(); buckets[bucketIndex] += entry.getValue();}System.out.printf('buckets: %sn', Arrays.toString(buckets)); } public static TreeMap<String, Integer> findBestDistribution(Map<String,Integer> symbolAndCount) {// 每個(gè)桶均勻分布的情況（最優(yōu)情況）int avg = symbolAndCount.values().stream().mapToInt(Integer::intValue).sum() / NUM_OF_BUCKETS;// 嘗試將 symbol 放入不同的桶int bucketIdx = 0;int[] buckets = new int[NUM_OF_BUCKETS];String[] bulkheads = new String[NUM_OF_BUCKETS-1];for (Map.Entry<String, Integer> entry : symbolAndCount.entrySet()) { // 如果首個(gè) symbol 數(shù)據(jù)量過大，則分配給其一個(gè)獨(dú)立的桶 int count = entry.getValue(); if (count / 2 > avg && bucketIdx == 0 && buckets[0] == 0) {buckets[bucketIdx] += count;continue; } // 評(píng)估將 symbol 放入桶后的效果 // 1. 如果桶中的數(shù)量更接近期望，則將其放入當(dāng)前桶中 // 2. 如果桶中的數(shù)量更遠(yuǎn)離期望，則將其放入下個(gè)桶中 double before = Math.abs(buckets[bucketIdx] - avg); double after = Math.abs(buckets[bucketIdx] + count - avg); if (after > before && bucketIdx < buckets.length - 1) {bulkheads[bucketIdx++] = entry.getKey(); } buckets[bucketIdx] += count;}System.out.printf('expectation: %dn', avg);System.out.printf('bulkheads: %sn', Arrays.toString(bulkheads));TreeMap<String,Integer> distribution = new TreeMap<>();for (int i=0; i<bulkheads.length; i++) { distribution.put(bulkheads[i], i+1);}return distribution; }}

該方法存在的問題：

分配策略并不是最優(yōu)解，且無法對(duì)其分片效果進(jìn)行直觀的評(píng)估。 當(dāng)區(qū)間數(shù)量較多時(shí)，查找表本身可能成為一個(gè)潛在的性能瓶頸。 可能的組合受到 key 的順序限制，極大地限制了可能的解空間。三、優(yōu)化 hash 函數(shù)

換個(gè)角度來看，造成分布不均勻的原因不是數(shù)據(jù)，而是 hash 函數(shù)本身。

項(xiàng)目中使用的 hash 函數(shù)是 JDK String 中的原生實(shí)現(xiàn)。經(jīng)過查閱資料，發(fā)現(xiàn)該實(shí)現(xiàn)其實(shí)是 BKDRHash 的 seed = 31 的特殊情況。這樣意味著：通過調(diào)整 seed 的值，可以改變 hash 函數(shù)的特性并使其適配特定的數(shù)據(jù)分布。

int BKDRHash(char[] value, int seed) { int hash = 0; for (int i = 0; i < value.length; i++) {hash = hash * seed + value[i]; } return hash & 0x7fffffff;}

那么問題來了，應(yīng)該如何評(píng)估某個(gè) seed 的分布的優(yōu)劣？

3.1、評(píng)價(jià)函數(shù)

一種可行的方法是計(jì)算每個(gè) seed 對(duì)應(yīng)的 bucket 分布的標(biāo)準(zhǔn)差，標(biāo)準(zhǔn)差越小則分布越均勻，則該 seed 越優(yōu)。

然而這一做法只考慮了每個(gè) bucket 與均值之間的誤差，無法量化不同 bucket 之間的誤差。為了能夠直觀的量化 bucket 之間分布差異的情況，考慮使用下面的評(píng)估函數(shù)：

ouble calculateDivergence(long[] bucket, long expectation) { long divergence = 0; for (int i=0; i<bucket.length; i++) {final long a = bucket[i];final long b = (a - expectation) * (a - expectation);for (int j=i+1; j<bucket.length; j++) { long c = (a - bucket[j]) * (a - bucket[j]); divergence += Math.max(b, c);} } return divergence; // the less the better}

該數(shù)值越小，則證明 seed 對(duì)應(yīng)的分布越均勻，其對(duì)應(yīng)的 hash 函數(shù)越優(yōu)。

3.2、訓(xùn)練策略

seed 是一個(gè) 32bit 的無符號(hào)整數(shù)，其取值范圍為 0 ～ 232-1。在 5000 個(gè) symbol 的情況下，單線程嘗試遍歷所有 seed 的時(shí)間約為 25 小時(shí)。

通常情況下 symbol 的數(shù)量會(huì)超過 5000，因此實(shí)際的搜索時(shí)間會(huì)大于這個(gè)值。此外，受限于計(jì)算資源限制，無法進(jìn)行大規(guī)模的并行搜索，因此窮舉法的耗時(shí)是不可接受的。

幸好本例并不要求最優(yōu)解，可以引入啟發(fā)式搜索算法，加快訓(xùn)練速度。由于本人在這方面并不熟悉，為了降低編程難度，最終選擇了模擬退火(simulated annealing)算法。它模擬固體退火過程的熱平衡問題與隨機(jī)搜索尋優(yōu)問題的相似性來達(dá)到尋找全局最優(yōu)或近似全局最優(yōu)的目的。相較于最簡(jiǎn)單的爬山法，模擬退火算法通以一定的概率接受較差的解，從而擴(kuò)大搜索范圍，保證解近似最優(yōu)。

/** * Basic framework of simulated annealing algorithm * @param <X> the solution of given problem */public abstract class SimulatedAnnealing<X> { protected final int numberOfIterations; // stopping condition for simulations protected final double coolingRate;// the percentage by which we reduce the temperature of the system protected final double initialTemperature; // the starting energy of the system protected final double minimumTemperature; // optional stopping condition protected final long simulationTime; // optional stopping condition protected final int detectionInterval; // optional stopping condition protected SimulatedAnnealing(int numberOfIterations, double coolingRate) {this(numberOfIterations, coolingRate, 10000000, 1, 0, 0); } protected SimulatedAnnealing(int numberOfIterations, double coolingRate, double initialTemperature, double minimumTemperature, long simulationTime, int detectionInterval) {this.numberOfIterations = numberOfIterations;this.coolingRate = coolingRate;this.initialTemperature = initialTemperature;this.minimumTemperature = minimumTemperature;this.simulationTime = simulationTime;this.detectionInterval = detectionInterval; } protected abstract double score(X currentSolution); protected abstract X neighbourSolution(X currentSolution); public X simulateAnnealing(X currentSolution) {final long startTime = System.currentTimeMillis();// Initialize searchingX bestSolution = currentSolution;double bestScore = score(bestSolution);double currentScore = bestScore;double t = initialTemperature;for (int i = 0; i < numberOfIterations; i++) { if (currentScore < bestScore) {// If the new solution is better, accept it unconditionallybestScore = currentScore;bestSolution = currentSolution; } else {// If the new solution is worse, calculate an acceptance probability for the worse solution// At high temperatures, the system is more likely to accept the solutions that are worseboolean rejectWorse = Math.exp((bestScore - currentScore) / t) < Math.random();if (rejectWorse || currentScore == bestScore) { currentSolution = neighbourSolution(currentSolution); currentScore = score(currentSolution);} } // Stop searching when the temperature is too low if ((t *= coolingRate) < minimumTemperature) {break; } // Stop searching when simulation time runs out if (simulationTime > 0 && (i+1) % detectionInterval == 0) {if (System.currentTimeMillis() - startTime > simulationTime) break; }}return bestSolution; }}/** * Search best hash seed for given key distribution and number of buckets with simulated annealing algorithm */@Datapublic class SimulatedAnnealingHashing extends SimulatedAnnealing<HashingSolution> { private static final int DISTRIBUTION_BATCH = 100; static final int SEARCH_BATCH = 200; private final int[] hashCodes = new int[SEARCH_BATCH]; private final long[][] buckets = new long[SEARCH_BATCH][]; @Data public class HashingSolution {private final int begin, range; // the begin and range for searchingprivate int bestSeed; // the best seed found in this searchprivate long bestScore; // the score corresponding to bestSeedprivate long calculateDivergence(long[] bucket) { long divergence = 0; for (int i=0; i<bucket.length; i++) {final long a = bucket[i];final long b = (a - expectation) * (a - expectation);for (int j=i+1; j<bucket.length; j++) { long c = (a - bucket[j]) * (a - bucket[j]); divergence += Math.max(b, c);} } return divergence; // the less the better}private HashingSolution solve() { if (range != hashCodes.length) {throw new IllegalStateException(); } for (int i=0; i<range; i++) {Arrays.fill(buckets[i], hashCodes[i] = 0); } for (KeyDistribution[] bucket : distributions) {for (KeyDistribution distribution : bucket) { Hashing.BKDRHash(distribution.getKey(), begin, hashCodes); for (int k = 0; k< hashCodes.length; k++) {int n = hashCodes[k] % buckets[k].length;buckets[k][n] += distribution.getCount(); }} } int best = -1; long bestScore = Integer.MAX_VALUE; for (int i = 0; i< buckets.length; i++) {long score = calculateDivergence(buckets[i]);if (i == 0 || score < bestScore) { bestScore = score; best = i;} } if (best < 0) {throw new IllegalStateException(); } this.bestScore = bestScore; this.bestSeed = begin + best; return this;}@Overridepublic String toString() { return String.format('(seed:%d, score:%d)', bestSeed, bestScore);} } private final KeyDistribution[][] distributions; // key and its count（2-dimensional array for better performance） private final long expectation; // the expectation count of each bucket private final int searchOutset; private int searchMin, searchMax; /** * SimulatedAnnealingHashing Prototype * @param keyAndCounts keys for hashing and count for each key * @param numOfBuckets number of buckets */ public SimulatedAnnealingHashing(Map<String, Integer> keyAndCounts, int numOfBuckets) {super(100000000, .9999);distributions = buildDistribution(keyAndCounts);long sum = 0;for (KeyDistribution[] batch : distributions) { for (KeyDistribution distribution : batch) {sum += distribution.getCount(); }}this.expectation = sum / numOfBuckets;this.searchOutset = 0;for (int i = 0; i< buckets.length; i++) { buckets[i] = new long[numOfBuckets];} } /** * SimulatedAnnealingHashing Derivative * @param prototype prototype simulation * @param searchOutset the outset for searching * @param simulationTime the expect time consuming for simulation */ private SimulatedAnnealingHashing(SimulatedAnnealingHashing prototype, int searchOutset, long simulationTime) {super(prototype.numberOfIterations, prototype.coolingRate, prototype.initialTemperature, prototype.minimumTemperature,simulationTime, 10000);distributions = prototype.distributions;expectation = prototype.expectation;for (int i = 0; i< buckets.length; i++) { buckets[i] = new long[prototype.buckets[i].length];}this.searchOutset = searchOutset;this.searchMax = searchMin = searchOutset; } @Override public String toString() {return String.format('expectation: %d, outset:%d, search(min:%d, max:%d)', expectation, searchOutset, searchMin, searchMax); } private KeyDistribution[][] buildDistribution(Map<String, Integer> symbolCounts) {int bucketNum = symbolCounts.size() / DISTRIBUTION_BATCH + Integer.signum(symbolCounts.size() % DISTRIBUTION_BATCH);KeyDistribution[][] distributions = new KeyDistribution[bucketNum][];int bucketIndex = 0;List<KeyDistribution> batch = new ArrayList<>(DISTRIBUTION_BATCH);for (Map.Entry<String, Integer> entry : symbolCounts.entrySet()) { batch.add(new KeyDistribution(entry.getKey().toCharArray(), entry.getValue())); if (batch.size() == DISTRIBUTION_BATCH) {distributions[bucketIndex++] = batch.toArray(new KeyDistribution[0]);batch.clear(); }}if (batch.size() > 0) { distributions[bucketIndex] = batch.toArray(new KeyDistribution[0]); batch.clear();}return distributions; } @Override protected double score(HashingSolution currentSolution) {return currentSolution.solve().bestScore; } @Override protected HashingSolution neighbourSolution(HashingSolution currentSolution) {// The default range of neighbourhood is [-100, 100]int rand = ThreadLocalRandom.current().nextInt(-100, 101);int next = currentSolution.begin + rand;searchMin = Math.min(next, searchMin);searchMax = Math.max(next, searchMax);return new HashingSolution(next, currentSolution.range); } public HashingSolution solve() {searchMin = searchMax = searchOutset;HashingSolution initialSolution = new HashingSolution(searchOutset, SEARCH_BATCH);return simulateAnnealing(initialSolution); } public SimulatedAnnealingHashing derive(int searchOutset, long simulationTime) {return new SimulatedAnnealingHashing(this, searchOutset, simulationTime); }}3.3、ForkJoin 框架

為了達(dá)到更好的搜索效果，可以將整個(gè)搜索區(qū)域遞歸地劃分為兩兩相鄰的區(qū)域，然后在這些區(qū)域上執(zhí)行并發(fā)的搜索，并遞歸地合并相鄰區(qū)域的搜索結(jié)果。

使用 JDK 提供的 ForkJoinPool 與 RecursiveTask 能很好地完成以上任務(wù)。

@Data@Slf4jpublic class HashingSeedCalculator { /** * Recursive search task */ private class HashingSeedCalculatorSearchTask extends RecursiveTask<HashingSolution> {private SimulatedAnnealingHashing simulation;private final int level;private final int center, range;private HashingSeedCalculatorSearchTask() { this.center = 0; this.range = Integer.MAX_VALUE / SimulatedAnnealingHashing.SEARCH_BATCH; this.level = traversalDepth; this.simulation = hashingSimulation;}private HashingSeedCalculatorSearchTask(HashingSeedCalculatorSearchTask parent, int center, int range) { this.center = center; this.range = range; this.level = parent.level - 1; this.simulation = parent.simulation;}@Overrideprotected HashingSolution compute() { if (level == 0) {long actualCenter = center * SimulatedAnnealingHashing.SEARCH_BATCH;log.info('Searching around center {}', actualCenter);HashingSolution solution = simulation.derive(center, perShardRunningMills).solve();log.info('Searching around center {} found {}', actualCenter, solution);return solution; } else {int halfRange = range / 2;int leftCenter = center - halfRange, rightCenter = center + halfRange;ForkJoinTask<HashingSolution> leftTask = new HashingSeedCalculatorSearchTask(this, leftCenter, halfRange).fork();ForkJoinTask<HashingSolution> rightTask = new HashingSeedCalculatorSearchTask(this, rightCenter, halfRange).fork();HashingSolution left = leftTask.join();HashingSolution right = rightTask.join();return left.getBestScore() < right.getBestScore() ? left : right; }} } private final int poolParallelism; private final int traversalDepth; private final long perShardRunningMills; private final SimulatedAnnealingHashing hashingSimulation; /** * HashingSeedCalculator * @param numberOfShards the shard of the whole search range [Integer.MIN_VALUE, Integer.MAX_VALUE] * @param totalRunningHours the expect total time consuming for searching * @param symbolCounts the key and it`s distribution * @param numOfBuckets the number of buckets */ public HashingSeedCalculator(int numberOfShards, int totalRunningHours, Map<String, Integer> symbolCounts, int numOfBuckets) {int n = (int) (Math.log(numberOfShards) / Math.log(2));if (Math.pow(2, n) != numberOfShards) { throw new IllegalArgumentException();}this.traversalDepth = n;this.poolParallelism = Math.max(ForkJoinPool.getCommonPoolParallelism() / 3 * 2, 1); // conservative estimation for parallelismthis.perShardRunningMills = TimeUnit.HOURS.toMillis(totalRunningHours * poolParallelism) / numberOfShards;this.hashingSimulation = new SimulatedAnnealingHashing(symbolCounts, numOfBuckets); } @Override public String toString() {int numberOfShards = (int) Math.pow(2, traversalDepth);int totalRunningHours = (int) TimeUnit.MILLISECONDS.toHours(perShardRunningMills * numberOfShards) / poolParallelism;return 'HashingSeedCalculator(' +'numberOfShards: ' + numberOfShards +', perShardRunningMinutes: ' + TimeUnit.MILLISECONDS.toMinutes(perShardRunningMills) +', totalRunningHours: ' + totalRunningHours +', poolParallelism: ' + poolParallelism +', traversalDepth: ' + traversalDepth + ')'; } public synchronized HashingSolution searchBestSeed() {long now = System.currentTimeMillis();log.info('SearchBestSeed start');ForkJoinTask<HashingSolution> root = new HashingSeedCalculatorSearchTask().fork();HashingSolution initSolution = hashingSimulation.derive(0, perShardRunningMills).solve();HashingSolution bestSolution = root.join();log.info('Found init solution {}', initSolution);log.info('Found best solution {}', bestSolution);if (initSolution.getBestScore() < bestSolution.getBestScore()) { bestSolution = initSolution;}long cost = System.currentTimeMillis() - now;log.info('SearchBestSeed finish (cost:{}ms)', cost);return bestSolution; }}3.4、效果

將改造后的代碼部署到測(cè)試環(huán)境后，某日訓(xùn)練日志：

12:49:15.227 85172866 INFO hash.HashingSeedCalculator - Found init solution (seed:15231, score:930685828341164)12:49:15.227 85172866 INFO hash.HashingSeedCalculator - Found best solution (seed:362333, score:793386389726926)12:49:15.227 85172866 INFO hash.HashingSeedCalculator - SearchBestSeed finish (cost:10154898ms)12:49:15.227 85172866 INFO hash.TrainingService -Training result: (seed:362333, score:793386389726926)Buckets: 15Expectation: 44045697Result of Hashing.HashCode(seed=362333): 21327108 [42512742, 40479608, 43915771, 47211553, 45354264, 43209190, 43196570, 44725786, 41999747, 46450288, 46079231, 45116615, 44004021, 43896194, 42533877]Result of Hashing.HashCode(seed=31): 66929172 [39723630, 48721463, 43365391, 46301448, 43931616, 44678194, 39064877, 45922454, 43171141, 40715060, 33964547, 49709090, 58869949, 34964729, 47581868]

當(dāng)晚使用 BKDRHash(seed=31) 對(duì)新的交易日數(shù)據(jù)的進(jìn)行分片：

04:00:59.001 partition messages per minute [45171, 68641, 62001, 80016, 55977, 61916, 55102, 49322, 55982, 57081, 51100, 70437, 135992, 37823, 58552] , messages total [39654953, 48666261, 43310578, 46146841, 43834832, 44577454, 38990331, 45871075, 43106710, 40600708, 33781629, 49752592, 58584246, 34928991, 47545369]

當(dāng)晚使用 BKDRHash(seed=362333) 對(duì)新的交易日數(shù)據(jù)的進(jìn)行分片：

04:00:59.001 partition messages per minute [62424, 82048, 64184, 47000, 57206, 69439, 64430, 60096, 46986, 58182, 54557, 41523, 64310, 72402, 100326] , messages total [44985772, 48329212, 39995385, 43675702, 45216341, 45524616, 41335804, 44917938, 44605376, 44054821, 43371892, 42068637, 44000817, 42617562, 44652695]

對(duì)比日志發(fā)現(xiàn) hash 經(jīng)過優(yōu)化后，分區(qū)的均勻程度有了顯著的上升，并且熱點(diǎn)分片也被消除了，基本達(dá)到當(dāng)初設(shè)想的優(yōu)化效果。

以上就是如何使用Java模擬退火算法優(yōu)化Hash函數(shù)的詳細(xì)內(nèi)容，更多關(guān)于Java 模擬退火算法優(yōu)化Hash的資料請(qǐng)關(guān)注好吧啦網(wǎng)其它相關(guān)文章！