Python求凸包及多邊形面積教程
一般有兩種算法來(lái)計(jì)算平面上給定n個(gè)點(diǎn)的凸包:Graham掃描法(Graham’s scan),時(shí)間復(fù)雜度為O(nlgn);Jarvis步進(jìn)法(Jarvis march),時(shí)間復(fù)雜度為O(nh),其中h為凸包頂點(diǎn)的個(gè)數(shù)。這兩種算法都按逆時(shí)針?lè)较蜉敵鐾拱旤c(diǎn)。
Graham掃描法
用一個(gè)棧來(lái)解決凸包問(wèn)題,點(diǎn)集Q中每個(gè)點(diǎn)都會(huì)進(jìn)棧一次,不符合條件的點(diǎn)會(huì)被彈出,算法終止時(shí),棧中的點(diǎn)就是凸包的頂點(diǎn)(逆時(shí)針順序在邊界上)。
算法步驟如下圖:
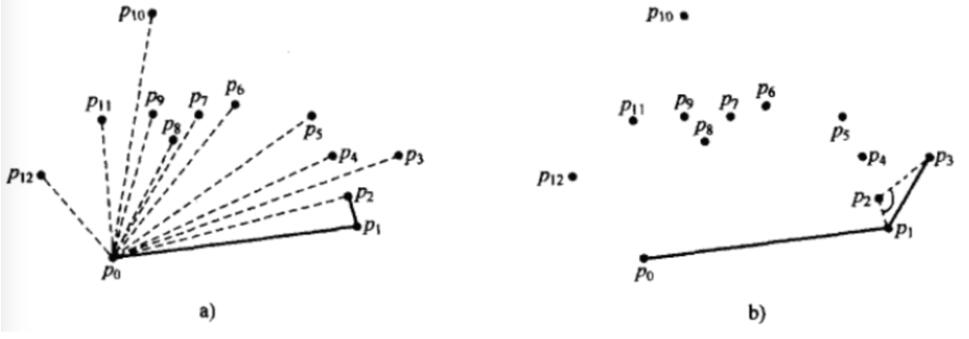
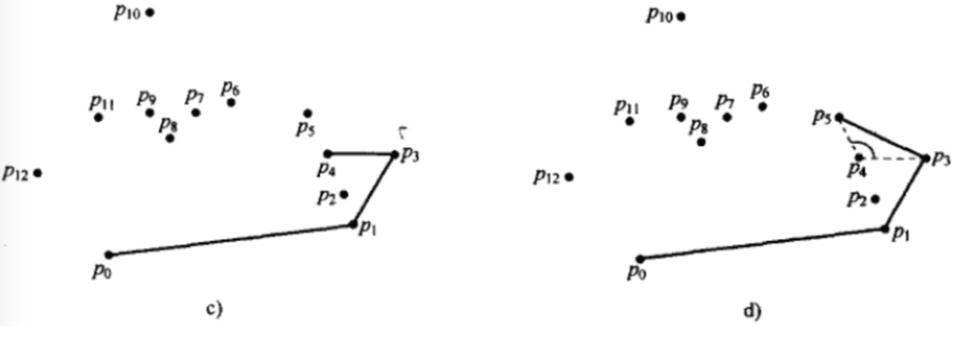
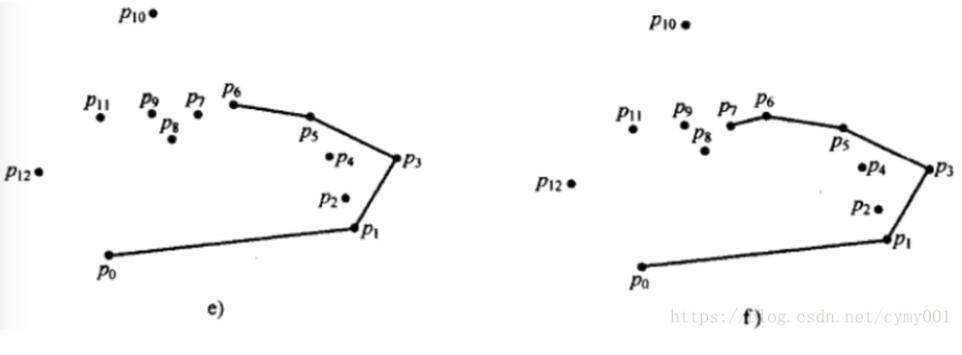
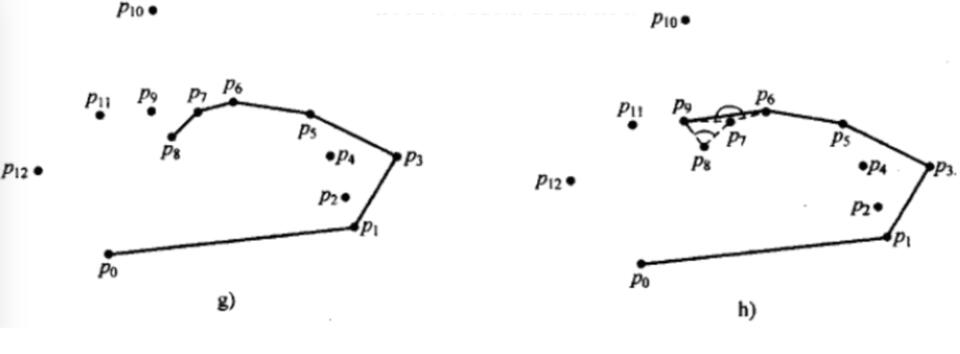
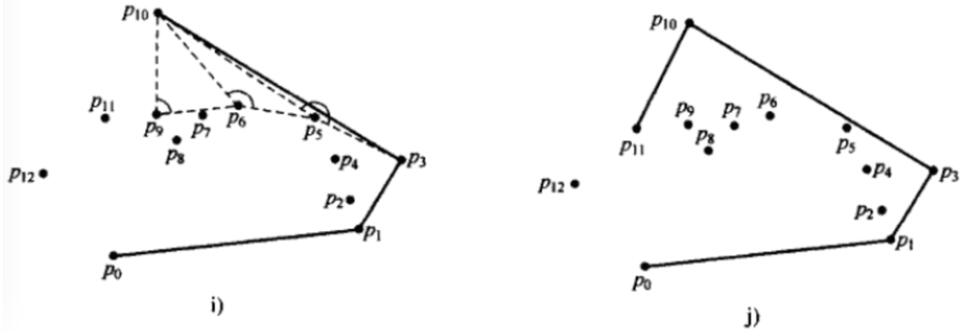
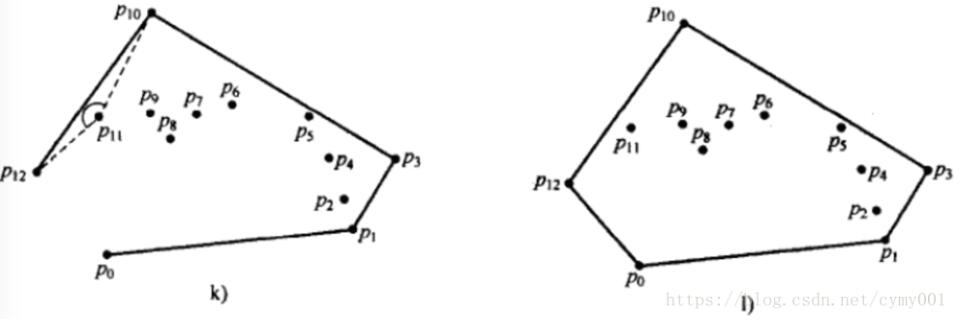
import sysimport mathimport timeimport random#獲取基準(zhǔn)點(diǎn)的下標(biāo),基準(zhǔn)點(diǎn)是p[k]def get_leftbottompoint(p): k = 0 for i in range(1, len(p)): if p[i][1] < p[k][1] or (p[i][1] == p[k][1] and p[i][0] < p[k][0]): k = i return k#叉乘計(jì)算方法def multiply(p1, p2, p0): return (p1[0] - p0[0]) * (p2[1] - p0[1]) - (p2[0] - p0[0]) * (p1[1] - p0[1])#獲取極角,通過(guò)求反正切得出,考慮pi/2的情況def get_arc(p1, p0): # 兼容sort_points_tan的考慮 if (p1[0] - p0[0]) == 0: if ((p1[1] - p0[1])) == 0: return -1; else: return math.pi / 2 tan = float((p1[1] - p0[1])) / float((p1[0] - p0[0])) arc = math.atan(tan) if arc >= 0: return arc else: return math.pi + arc#對(duì)極角進(jìn)行排序,排序結(jié)果list不包含基準(zhǔn)點(diǎn)def sort_points_tan(p, pk): p2 = [] for i in range(0, len(p)): p2.append({'index': i, 'arc': get_arc(p[i], pk)}) #print(’排序前:’,p2) p2.sort(key=lambda k: (k.get(’arc’))) #print(’排序后:’,p2) p_out = [] for i in range(0, len(p2)): p_out.append(p[p2[i]['index']]) return p_outdef convex_hull(p): p=list(set(p)) #print(’全部點(diǎn):’,p) k = get_leftbottompoint(p) pk = p[k] p.remove(p[k]) #print(’排序前去除基準(zhǔn)點(diǎn)的所有點(diǎn):’,p,’基準(zhǔn)點(diǎn):’,pk) p_sort = sort_points_tan(p, pk) #按與基準(zhǔn)點(diǎn)連線和x軸正向的夾角排序后的點(diǎn)坐標(biāo) #print(’其余點(diǎn)與基準(zhǔn)點(diǎn)夾角排序:’,p_sort) p_result = [pk,p_sort[0]] top = 2 for i in range(1, len(p_sort)): ##################################### #叉乘為正,向前遞歸刪點(diǎn);叉乘為負(fù),序列追加新點(diǎn) while(multiply(p_result[-2], p_sort[i],p_result[-1]) > 0): p_result.pop() p_result.append(p_sort[i]) return p_result#測(cè)試
if __name__ == ’__main__’: pass test_data = [(220, -100), (0,0), (-40, -170), (240, 50), (-160, 150), (-210, -150)] print(test_data) result = convex_hull(test_data) print(result) t=0import matplotlib.pyplot as pltx1=[]y1=[]for i in range(len(test_data)): ri=test_data[i] #print(ri) x1.append(ri[0]) y1.append(ri[1])plt.plot(x1,y1,linestyle=’ ’,marker=’.’)xx=[]yy=[]for i in range(len(result)): ri=result[i] #print(ri) xx.append(ri[0]) yy.append(ri[1])plt.plot(xx,yy,linestyle=’ ’,marker=’*’)
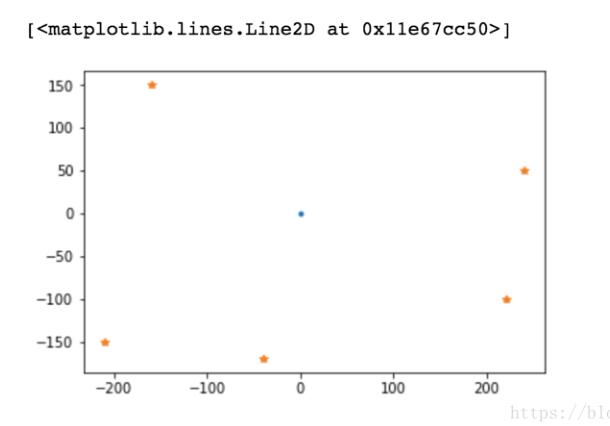
計(jì)算多邊形面積
(1)順時(shí)針給定構(gòu)成凸包的n個(gè)點(diǎn)坐標(biāo),叉乘法求多邊形面積:

def GetAreaOfPolyGonbyVector(points): # 基于向量叉乘計(jì)算多邊形面積 area = 0 if(len(points)<3): raise Exception('error') for i in range(0,len(points)-1): p1 = points[i] p2 = points[i + 1] triArea = (p1[0]*p2[1] - p2[0]*p1[1])/2 #print(triArea) area += triArea fn=(points[-1][0]*points[0][1]-points[0][0]*points[-1][1])/2 #print(fn) return abs(area+fn)points = []x = [1,3,2]y = [1,2,2] #[(1,1),(3,1),(5,3),(3,5),(1,3)] # x=[1,3,5,3,1]# y=[1,1,3,5,3]for index in range(len(x)): points.append((x[index],y[index]))area = GetAreaOfPolyGonbyVector(points)print(area)#print(math.ceil(area))
(2)順時(shí)針給定構(gòu)成凸包的n個(gè)點(diǎn)經(jīng)緯度坐標(biāo),先將經(jīng)緯度坐標(biāo)轉(zhuǎn)化成凸多邊形的邊的經(jīng)緯度距離,利用海倫公式求多邊形面積:
from geopy.distance import vincentyimport mathdef HeronGetAreaOfPolyGonbyVector(points): # 基于海倫公式計(jì)算多邊形面積 area = 0 if(len(points)<3): raise Exception('error') pb=((points[-1][0]+points[0][0])/2,(points[-1][1]+points[0][1])/2) #基準(zhǔn)點(diǎn)選為第一個(gè)點(diǎn)和最后一個(gè)點(diǎn)連線邊上的中點(diǎn) for i in range(0,len(points)-1): p1 = points[i] p2 = points[i + 1] db1 = vincenty(pb,p1).meters #根據(jù)維度轉(zhuǎn)化成經(jīng)緯度距離 d12 = vincenty(p1,p2).meters d2b = vincenty(p2,pb).meters #print(db1,d12,d2b) hc = (db1+d12+d2b)/2 #db1是基準(zhǔn)點(diǎn)和p1的距離,d12是p1和p2的距離,d2b是p2和基準(zhǔn)點(diǎn)距離 #print(hc, hc-db1, hc-d12, hc-d2b) triArea = math.sqrt(hc*(hc-db1)*(hc-d12)*(hc-d2b)) #print(triArea) area += triArea return areapoints = []x = [1,3,2]y = [1,2,2] #[(1,1),(3,1),(5,3),(3,5),(1,3)] # x=[1,3,5,3,1]# y=[1,1,3,5,3]for index in range(len(x)): points.append((x[index],y[index]))area = HeronGetAreaOfPolyGonbyVector(points)print(area)#print(math.ceil(area))
Graham程序原理
(1)基準(zhǔn)點(diǎn)的確認(rèn)原則:
有唯一的某個(gè)點(diǎn)縱坐標(biāo)最小,該點(diǎn)為基準(zhǔn)點(diǎn);
不止一個(gè)點(diǎn)的縱坐標(biāo)最小,選這些點(diǎn)里最靠左的為基準(zhǔn)點(diǎn)
(2)計(jì)算叉乘【后續(xù)利用叉乘正負(fù)判斷夾角是否大于180o】:
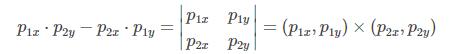
(3)獲取極角,通過(guò)求反正切得出:
若橫縱坐標(biāo)都相等(兩點(diǎn)相同),返回-1;
若橫坐標(biāo)相等/縱坐標(biāo)不相等(兩點(diǎn)連線垂直y軸),返回 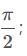
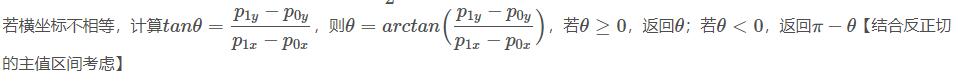
(4)對(duì)極角進(jìn)行排序,排序結(jié)果list不包含基準(zhǔn)點(diǎn):
p2=[{'index':0, 'arc':get_arc(p[0],p[k])}, {'index':1, 'arc':get_arc(p[1],p[k])}, ··· {'index':k-1, 'arc':get_arc(p[k-1],p[k])}, {'index':k+1, 'arc':get_arc(p[k+1],p[k])}, ··· {'index':n, 'arc':get_arc(p[n],p[k])}]#get_arc(p[0],p[k])即獲得p[0]點(diǎn)與基準(zhǔn)點(diǎn)p[k]連線的極角(與x軸正向夾角)#根據(jù)p2的“arc”鍵的值從小到大排序,最后輸出按該角度值排序?qū)?yīng)順序的各個(gè)點(diǎn)
(5)逆時(shí)針確定凸多邊形:
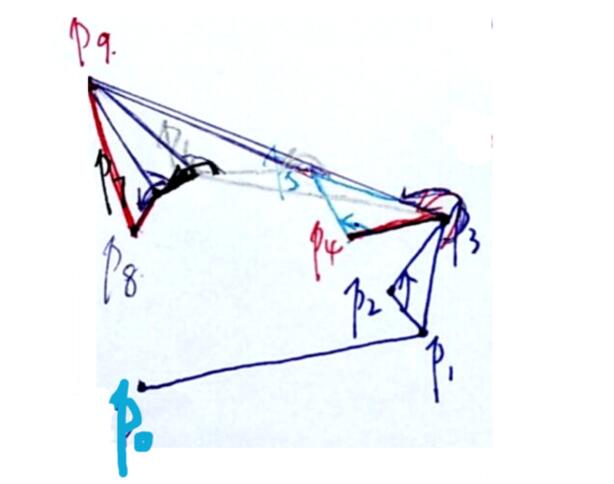
主要是找角度是否大于180o——差乘正負(fù)——點(diǎn)進(jìn)出棧順序三者關(guān)系

...一直遍歷到最后一個(gè)點(diǎn)...一直遍歷到最后一個(gè)點(diǎn)
規(guī)律:叉乘>0,夾角小于180o,遞歸向前刪點(diǎn);叉乘<0,夾角大于180o,不刪點(diǎn),加入新點(diǎn),向后遍歷叉乘>0,夾角小于180o,遞歸向前刪點(diǎn);叉乘<0,夾角大于180o,不刪點(diǎn),加入新點(diǎn),向后遍歷
注意:(a)上述給非基準(zhǔn)點(diǎn)按極角從到大小排號(hào)時(shí),有兩個(gè)及以上點(diǎn)“和基準(zhǔn)點(diǎn)連線構(gòu)成的極角”相等時(shí),這些點(diǎn)的排號(hào)挨著但是沒(méi)有固定順序,這點(diǎn)并不影響算法給出凸包的準(zhǔn)確性。(b)對(duì)排號(hào)最后的一個(gè)點(diǎn),掃描算法里沒(méi)有任何刪除該點(diǎn)的機(jī)制,但是這點(diǎn)也不影響算法給出凸包的準(zhǔn)確性。(c)上述程序需要額外加入,判斷結(jié)束棧內(nèi)點(diǎn)數(shù)小于3和篩選凸包前點(diǎn)數(shù)小于3,不能計(jì)算多邊形面積的情況,可以直接給這種情況賦值0返回。
以上這篇Python求凸包及多邊形面積教程就是小編分享給大家的全部?jī)?nèi)容了,希望能給大家一個(gè)參考,也希望大家多多支持好吧啦網(wǎng)。
相關(guān)文章:
1. 測(cè)試模式 - XSL教程 - 52. 用xslt+css讓RSS顯示的跟網(wǎng)頁(yè)一樣漂亮3. CSS3實(shí)現(xiàn)動(dòng)態(tài)翻牌效果 仿百度貼吧3D翻牌一次動(dòng)畫(huà)特效4. 《CSS3實(shí)戰(zhàn)》筆記--漸變?cè)O(shè)計(jì)(一)5. 移動(dòng)端HTML5實(shí)現(xiàn)拍照功能的兩種方法6. 讓chatgpt將html中的圖片轉(zhuǎn)為base64方法示例7. html5手機(jī)觸屏touch事件介紹8. ASP.NET Core自定義中間件的方式詳解9. ASP.NET MVC把數(shù)據(jù)庫(kù)中枚舉項(xiàng)的數(shù)字轉(zhuǎn)換成文字10. 教你JS更簡(jiǎn)單的獲取表單中數(shù)據(jù)(formdata)

 網(wǎng)公網(wǎng)安備
網(wǎng)公網(wǎng)安備