這是刷題時遇到的一道題，題目描述：小Q定義了一種數(shù)列稱為翻轉數(shù)列:

給定整數(shù)n和m, 滿足n能被2m整除。對于一串連續(xù)遞增整數(shù)數(shù)列1, 2, 3, 4..., 每隔m個符號翻轉一次, 最初符號為’-’;。

例如n = 8, m = 2, 數(shù)列就是: -1, -2, +3, +4, -5, -6, +7, +8.

而n = 4, m = 1, 數(shù)列就是: -1, +2, -3, + 4.

小Q現(xiàn)在希望你能幫他算算前n項和為多少。

如果只需求出N項和的話，這里可以有一個簡便思路，觀察規(guī)律哈，比如n = 8, m = 2, 數(shù)列就是: -1, -2, +3, +4, -5, -6, +7, +8.時，

思路1：

對于一次翻轉前后的兩個子數(shù)組， -1, -2, 和+3, +4，+3和-1的和為2，+4和-2的和為2，總和為4，同理對后面的兩個子數(shù)組求和也是4，也就是說，前后兩個不同符號的子數(shù)組的和剛好是M*M，那么這樣的數(shù)組有多少呢，有N／２Ｍ次，所以和為M*N/2

思路2：

對于相隔m個的兩個數(shù)字數(shù)字的正好為M,這樣的數(shù)字對有N/2個，所以和就為M*N/2啦~~~~是不是so easy呀

好了，python實現(xiàn)如下，這個是把數(shù)列輸出，然后再求和，另外思路2在里面有體現(xiàn)哦

def isInput(m,n): c=n/m d=c%2 if d==0: return True else: return Falsedef s(m,n): t=int(n/m) an=[] ai=0 for turntime in range(1,t+1):#turntime是翻轉次數(shù) for sublen in range(0,m):#sublen是相同符號的子序列長度 ai=ai+1 tt=turntime%2 if tt==0: an.append(ai) else: ci=ai*(-1) an.append(ci) print(an) print(sum(an)) test=[] for a in an: if a<0: test.append(a) x=len(test) print(m*x)#這里可以直接計算出結果m=int(input('請輸入M:'))n=int(input(’請輸入N:’))if isInput(m,n)==False: print(’輸入不合法’)else: s(m,n)

補充知識：Python Fibonacci-無窮數(shù)列 求第n項及前n項和

Fibonacci數(shù)列，又稱無窮列表，前n項和為：1,1,2,3,5,8,13,21,34,55…

他可以遞歸地定義為：

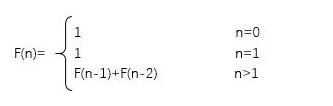
這是一個遞歸關系，當n大于1時，這個數(shù)列的第n項和是前兩項之和。利用遞歸算法可以很簡單地解出其解以及前n項和。

# 分段函數(shù) F（n）= {1 n=0; 1 n=1; F(n-1)+F(-2) n>1}def backValue(n): if n<=1: return 1 return backValue(n-1)+backValue(n-2)n = int(input('輸入一個大于 0 的正整數(shù)：'))value = [i for i in range(n)]Fbc_list = []for i in value: s = backValue(i) Fbc_list.append(s)print('第%s的數(shù)為：'%n,Fbc_list[-1],'n無窮列表為：',Fbc_list,'n前%s項和為：'%n,sum(Fbc_list))

以上這篇翻轉數(shù)列python實現(xiàn),求前n項和,并能輸出整個數(shù)列的案例就是小編分享給大家的全部內容了，希望能給大家一個參考，也希望大家多多支持好吧啦網(wǎng)。