在深度學(xué)習(xí)出來之前，圖像識別領(lǐng)域北有“Gabor幫主”，南有“SIFT慕容小哥”。目前，深度學(xué)習(xí)技術(shù)可以利用CNN網(wǎng)絡(luò)和大數(shù)據(jù)樣本搞事情，從而取替“Gabor幫主”和“SIFT慕容小哥”的江湖地位。但，在沒有大數(shù)據(jù)和算力支撐的“鄉(xiāng)村小鎮(zhèn)”地帶，或是對付“刁民小輩”，“Gabor幫主”可以大顯身手，具有不可撼動的地位。IT武林中，有基于C++和OpenCV，或是基于matlab的Gabor圖像變換與特征提取源代碼，但大多招數(shù)花哨。而基于Python語言的Gabor圖像變換和特征提取卻很少見。本博主在實現(xiàn)基于Python語言的Gabor圖像變換和特征提取中發(fā)現(xiàn)其確實比OpenCV或matlab務(wù)實，話少人狠，特和大家分享。

“Gabor幫主”最厲害的武器是Gabor濾波器，其最主要使用優(yōu)勢體現(xiàn)在對物體紋理特征的提取上。Gabor濾波器對于圖像的亮度和對比度變化以及圖像姿態(tài)變化具有較強的魯棒性，并且它表達(dá)的是對圖像識別最為有用的局部特征，故在計算機視覺及紋理分析領(lǐng)域中得到廣泛的應(yīng)用。Gabor濾波器可以提取不同方向和不同尺度的上的特征，并且進(jìn)行隨意組合，變幻莫測。下圖為4個方向（0o，45o，90o，135o）和6個尺度（7，9，11，13，15，17），組合生成的24個Gabor濾波核。

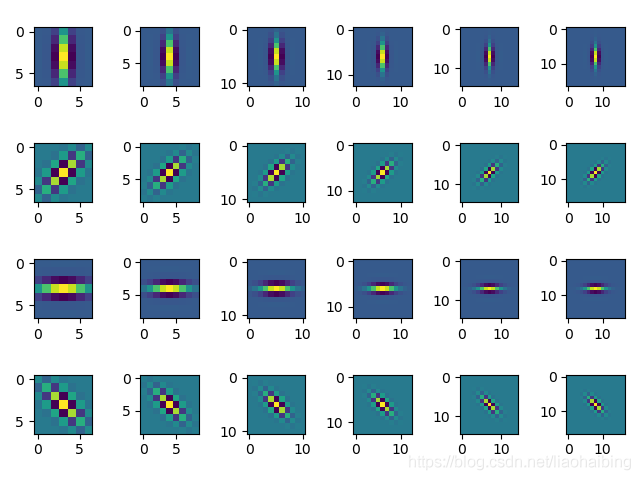
所謂Gabor圖像變換就使用Gabor濾波器對圖像進(jìn)行濾波操作（相當(dāng)于CNN中的卷積操作）得到新的圖像。每個濾波核與圖像濾波之后得到：

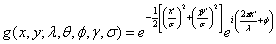
其中，λ為波，它的值以像素為單位指定，通常大于等于2。但不能大于輸入圖像尺寸的五分之一；θ為方向，指定了Gabor函數(shù)并行條紋的方向，它的取值為0到2π；ϕ為相位偏移，它的取值范圍為−π到π。其中，0、π度分別對應(yīng)中心對稱的center-on函數(shù)和center-off函數(shù)，而-π/2和π/2對應(yīng)反對稱函數(shù)；γ為長寬比，空間縱橫比，決定了Gabor函數(shù)形狀的橢圓率，當(dāng)γ=1時，形狀是圓的，當(dāng)γ<1時，形狀隨著平行條紋方向而拉長，通常該值為0.5；σ表示Gabor函數(shù)的高斯因子的標(biāo)準(zhǔn)差，它的值不能直接設(shè)置，它僅隨著帶寬b變化，帶寬值必須是正實數(shù)，通常為1，此時，標(biāo)準(zhǔn)差和波長的關(guān)系為：σ=0.56λ；帶寬（b）：Gabor濾波器的半響應(yīng)空間頻率帶寬：

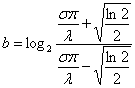
x’,y’的值為：

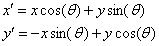
gabor濾波核是復(fù)數(shù)形式，因此可以把它分開成實部和虛部：

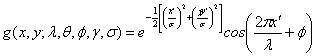
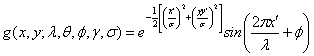
弄清以上公式原理后，大家也可以自己嘗試?yán)肞ython把Gabor變換實現(xiàn)，源代碼我這里就不貼了，如果大家感興趣，可以參考https://www.jb51.net/article/198212.htm。其實，skimage包中就有封裝好的gabor變換函數(shù)，可以直接調(diào)用。因此，這里介紹一種簡單偷懶的方式。從skimage中導(dǎo)入filters（from skimage import filters)后,便可調(diào)用gabor函數(shù)了，其函數(shù)說明如下：skimage.filters.gabor(image, frequency, theta=0, bandwidth=1, sigma_x=None, sigma_y=None, n_stds=3, offset=0, mode=‘reflect’, cval=0)1）函數(shù)返回：Gabor變換后的實部和虛部real，imag；大小與輸入圖像尺寸相同。2）函數(shù)參數(shù)：圖像（image）：二維數(shù)組輸入圖像（灰度圖像）；頻率（frequency）：浮點諧波函數(shù)的空間頻率，控制尺度；

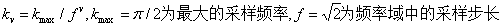
，在圖像特征提取領(lǐng)域通常取5個不同尺度

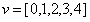
方向（theta）：float，可選的弧度方向，如果為0，則諧波處于x方向；

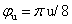
，在圖像特征提取領(lǐng)域通常取8個不同方向u=[0,1,2,3,4,5,6,7]。帶寬（bandwidth)：浮點，可選由過濾器捕獲的帶寬。對于固定帶寬，sigma_x和sigma_y將隨著頻率的增加而降低，如果用戶設(shè)置了sigma_x和sigma_y，則該值將被忽略；標(biāo)準(zhǔn)偏差(sigma_x，sigma_y)：float，x和y方向上的可選標(biāo)準(zhǔn)偏差；內(nèi)核的線性大小(n_stds)：標(biāo)量，可選內(nèi)核的線性大小為n_stds（默認(rèn)為3）標(biāo)準(zhǔn)偏差；偏移量(offset)：浮點數(shù)，可選項以弧度表示的諧波函數(shù)的相位偏移；模式(mode）：{‘constant’，‘near’，‘reflect’，‘mirror’，‘wrap’}，可選用于將圖像與內(nèi)核進(jìn)行卷積的模式，傳遞給ndi.convolve；cval：標(biāo)量，可選值如果卷積模式為’不變’，該參數(shù)被傳遞給ndi.convolve。3）源代碼如下：

import matplotlib.pyplot as pltfrom skimage import filters,io,colorimport numpy as npfilename=’D:/lena.jpg’img = io.imread(filename)#讀取圖像img_gray = color.rgb2gray(img)#RGB轉(zhuǎn)灰度frequency=0.6#調(diào)用gabor函數(shù)real, imag = filters.gabor(img_gray, frequency=0.6,theta=45,n_stds=5)#取模圖像img_mod=np.sqrt(real.astype(float)**2+imag.astype(float)**2)#圖像顯示plt.figure()plt.subplot(2,2,1)plt.imshow(img_gray,cmap=’gray’)plt.subplot(2,2,2)plt.imshow(img_mod,cmap=’gray’)plt.subplot(2,2,3)plt.imshow(real,cmap=’gray’)plt.subplot(2,2,4)plt.imshow(imag,cmap=’gray’)plt.show()

4）運行結(jié)果如下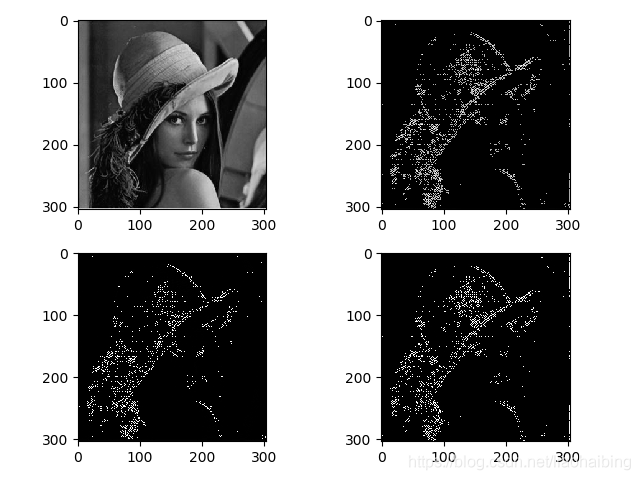：5）注意事項①通過theta參數(shù)調(diào)不同方向，這里輸入是弧度，不是角度。②通過frequency參數(shù)調(diào)不同尺度變化。6）利用skimage生成gobor卷積核：gabor_kernelskimage.filters.gabor_kernel(frequency, theta=0, bandwidth=1, sigma_x=None, sigma_y=None, n_stds=3, offset=0)函數(shù)返回：返回2D Gabor濾波器內(nèi)核，包含實部與虛部。參數(shù)與skimage.filters.gabor（）函數(shù)相同。源代碼如下：

import matplotlib.pyplot as pltfrom skimage import filtersgk = filters.gabor_kernel(frequency=0.1,theta=np.pi*30/180.0,n_stds=5)mod=np.sqrt(gk.real.astype(float) ** 2 + gk.imag.astype(float) ** 2)plt.figure()plt.subplot(1,3,1)plt.imshow(gk.real*255,cmap=’gray’)plt.subplot(1,3,2)plt.imshow(gk.imag*255,cmap=’gray’)plt.subplot(1,3,3)plt.imshow(mod*255,cmap=’gray’)plt.show()

運行結(jié)果如下：

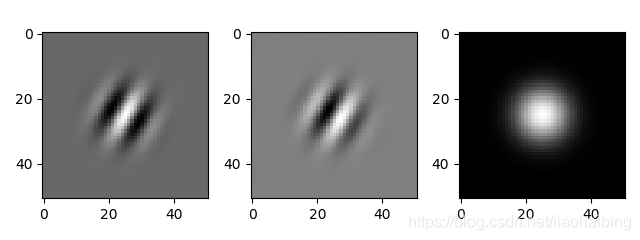
注意事項：①參數(shù)n_stds=3并不是說濾波核大小為（3,3)，濾波核大小由參數(shù)frequency、theta、n_stds三個參數(shù)共同決定。②gabor_kernel函數(shù)返回是帶有實部和虛部的復(fù)矩陣。③theta是弧度，不是角度

3.“Gabor幫主”大招之圖像特征提取

Gabor濾波器可以在頻域上不同尺度、不同方向上提取相關(guān)的特征。另外，Gabor函數(shù)與人眼的作用相仿，所以經(jīng)常用作紋理識別上，并取得了較好的效果。Gabor特征提取一般包括取模、特征降維、特征歸一化和特征選取等操作：取模：skimage.filters.gabor（）函數(shù)返回的是圖像變換后的實部和虛部，在圖像識別領(lǐng)域一般使用其模作為圖像特征

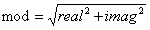
2）特征降維：skimage.filters.gabor（）函數(shù)返回值大小和原圖像一樣；另外，圖像識別領(lǐng)域一般使用8個方向和5個尺度的gabor濾波器，得到40幅變換圖像；導(dǎo)致提取的圖像特征維度（40幅圖像特征串聯(lián)）比較高。因此，需要對取模圖像進(jìn)行降維處理。最簡單的方法就是對每個模圖像進(jìn)行下采樣，如使用Opencv中的resize函數(shù)cv2.resize(img,(0,0),fx=1/4,fy=1/4)。3）特征歸一化：在機器學(xué)習(xí)領(lǐng)域中，不同評價指標(biāo)（即特征向量中的不同特征就是所述的不同評價指標(biāo)）往往具有不同的量綱和量綱單位，這樣的情況會影響到數(shù)據(jù)分析的結(jié)果，為了消除指標(biāo)之間的量綱影響，需要進(jìn)行數(shù)據(jù)標(biāo)準(zhǔn)化處理，以解決數(shù)據(jù)指標(biāo)之間的可比性。原始數(shù)據(jù)經(jīng)過數(shù)據(jù)標(biāo)準(zhǔn)化處理后，各指標(biāo)處于同一數(shù)量級，適合進(jìn)行綜合對比評價。其中，最典型的就是數(shù)據(jù)的歸一化處理。簡而言之，歸一化的目的就是使得預(yù)處理的數(shù)據(jù)被限定在一定的范圍內(nèi)。本博主介紹一種Z-score標(biāo)準(zhǔn)化方法：當(dāng)一化公式：

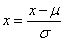
其中μ為所有樣本數(shù)據(jù)的均值，σ為所有樣本數(shù)據(jù)的標(biāo)準(zhǔn)差。b）本方法要求原始數(shù)據(jù)的分布可以近似為高斯分布，否則歸一化的效果會變得很糟糕；c）應(yīng)用場景：在分類、聚類算法中，需要使用距離來度量相似性的時候、或者使用PCA技術(shù)進(jìn)行降維的時候，Z-score standardization表現(xiàn)更好。4）特征選取經(jīng)過以上三步后，可以將各模圖像特征串聯(lián)起來作為輸入圖像的特征向量。但此時得到的特征向量存在大量冗余，最好再進(jìn)行一次特征降維（特征選取）操作。可以采用PCA或Fisher等線性子空間分析方法。5）源代碼：

import cv2import numpy as npfrom skimage import filtersfilename=’D:/lena.jpg’img = cv2.imread(filename)#讀圖像img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)#轉(zhuǎn)灰度frequency=0.6#gabor變換real, imag = filters.gabor(img_gray, frequency=0.6,theta=45,n_stds=5)#取模img_mod=np.sqrt(real.astype(float)**2+imag.astype(float)**2)#圖像縮放（下采樣）newimg = cv2.resize(img_mod,(0,0),fx=1/4,fy=1/4,interpolation=cv2.INTER_AREA)tempfea = newimg.flatten()#矩陣展平tmean = np.mean(tempfea)#求均值tstd = np.std(tempfea)#求方差newfea = (tempfea - tmean)/tstd#數(shù)值歸一化print(newfea)

夜已深，公司都沒有一個人了，空蕩蕩的。先寫到這里吧，第一次在CSDN上發(fā)博文，有不到之處請指正，如果您覺得還有點用，請點個贊以支鼓勵，不勝感激！！！！

到此這篇關(guān)于詳解基于python的圖像Gabor變換及特征提取的文章就介紹到這了,更多相關(guān)python Gabor變換及特征提取內(nèi)容請搜索好吧啦網(wǎng)以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持好吧啦網(wǎng)！