對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序，是將G中所有頂點排成一個線性序列，使得圖中任意一對頂點u和v，若邊(u,v)∈E(G)，則u在線性序列中出現在v之前。

通常，這樣的線性序列稱為滿足拓撲次序(Topological Order)的序列，簡稱拓撲序列。簡單的說，由某個集合上的一個偏序得到該集合上的一個全序，這個操作稱之為拓撲排序。

在圖論中，由一個有向無環圖的頂點組成的序列，當且僅當滿足下列條件時，稱為該圖的一個拓撲排序（英語：Topological sorting）：

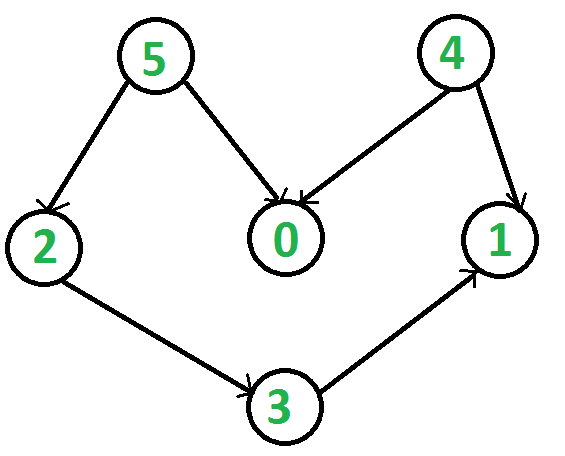
實例代碼

from collections import defaultdict class Graph: def __init__(self,vertices): self.graph = defaultdict(list) self.V = vertices def addEdge(self,u,v): self.graph[u].append(v) def topologicalSortUtil(self,v,visited,stack): visited[v] = True for i in self.graph[v]: if visited[i] == False: self.topologicalSortUtil(i,visited,stack) stack.insert(0,v) def topologicalSort(self): visited = [False]*self.V stack =[] for i in range(self.V): if visited[i] == False: self.topologicalSortUtil(i,visited,stack) print (stack) g= Graph(6) g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); print ('拓撲排序結果：')g.topologicalSort()

執行以上代碼輸出結果為：

拓撲排序結果：

[5, 4, 2, 3, 1, 0]

實例擴展：

def toposort(graph): in_degrees = dict((u,0) for u in graph) #初始化所有頂點入度為0 vertex_num = len(in_degrees) for u in graph: for v in graph[u]: in_degrees[v] += 1 #計算每個頂點的入度 Q = [u for u in in_degrees if in_degrees[u] == 0] # 篩選入度為0的頂點 Seq = [] while Q: u = Q.pop() #默認從最后一個刪除 Seq.append(u) for v in graph[u]: in_degrees[v] -= 1 #移除其所有指向 if in_degrees[v] == 0: Q.append(v) #再次篩選入度為0的頂點 if len(Seq) == vertex_num: #如果循環結束后存在非0入度的頂點說明圖中有環，不存在拓撲排序 return Seq else: print('there’s a circle.')G = { ’a’:’bce’, ’b’:’d’, ’c’:’d’, ’d’:’’, ’e’:’cd’}print(toposort(G))

輸出結果：

[’a’, ’e’, ’c’, ’b’, ’d’]

到此這篇關于Python關于拓撲排序知識點講解的文章就介紹到這了,更多相關Python 拓撲排序內容請搜索好吧啦網以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持好吧啦網！